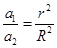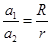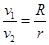题目内容
一颗人造地球卫星在地面附近绕地球做匀速圆周运动的速率为v，角速度为ω，加速度为g，周期为T。另一颗人造地球卫星在离地面高度为地球半径的轨道上做匀速圆周运动， 则（ ）
A．它的速率为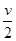 | B．它的加速度为 |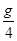
C．它的运动周期为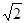 T | D．它的角速度也为ω |
B
解析试题分析：A、研究地面附近的卫星绕地球做匀速圆周运动，根据万有引力提供向心力，列出等式：
①，
R为地球半径，M为地球质量，V为卫星的速率．研究另一个卫星绕地球做匀速圆周运动，根据万有引力提供向心力，列出等式：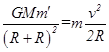
②
由①②得：v′=
v，故A错误．
B、忽略地球自转的影响，根据万有引力等于重力列出等式：
mg，g=
g′=
，故B正确．
C、研究地面附近的卫星绕地球做匀速圆周运动，根据万有引力提供向心力，列出等式：
，T=2π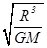
,另一个卫星的周期T′=2π
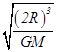≠T，故C错误．
D、地面附近的卫星的周期与另一个卫星的周期不等，根据ω=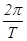
得它们的角速度也不等．故D错误．
考点：万有引力定律及其应用．
名校课堂系列答案把火星和地球绕太阳运行的轨道视为圆周，由火星和地球绕太阳运动的周期之比可求得（ ）
| A．火星和地球的质量之比 |
| B．火星和太阳的质量之比 |
| C．火星和地球到太阳的距离之比 |
| D．火星和地球绕太阳运行速度大小之比 |
假设地球的质量不变，半径增大到原来的2倍，那么从地球发射人造卫星的第一宇宙速度的大小应为原来的
A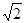． 倍 | B． 倍 | C．1/2倍 | D．2倍 |
下面说法中正确的是
| A．第一宇宙速度是人造地球卫星绕地飞行的最大速度 |
B．若地球半径为R，地面重力加速度为g，则卫星在距地面高度R处的加速度为 |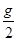
| C．卫星在高轨道上的速率大于在低轨道上的速率 |
| D．同步卫星一定位于空间不同轨道上 |
已知万有引力恒量G后，要计算地球的质量，还必须知道某些数据，现在给出下列各组数据，可以算出地球质量的有（ ）
| A．地球绕太阳运行的周期T和地球离太阳中心的距离r |
| B．月球绕地球运行的周期T和月球离地球中心的距离r |
| C．人造地球卫星在地面附近运行的速度和运动周期T |
| D．同步卫星离地面的高度 |
太空中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统，通常可忽略其它星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式：一种是三颗星位于同一直线上，两颗星围绕中央星在同一半径为R的圆轨道上运行；另一种形式是三颗星位于等边三角形的三个顶点上，并沿外接于等边三角形的圆形轨道运行。设这三个星体的质量均为M，并设两种系统的运动周期相同，则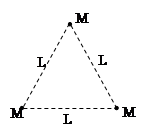
A．直线三星系统运动的线速度大小为 |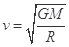
B．此三星系统的运动周期为 |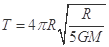
C．三角形三星系统中星体间的距离为 |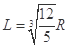
D．三角形三星系统的线速度大小为 |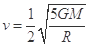
“月亮女神”沿距月球表面100km的轨道做匀速圆周飞行，“嫦娥一号”沿距月球表面200km的轨道做匀速圆周飞行，下列说法正确的是
| A．“月亮女神”的周期小于“嫦娥一号”的周期 |
| B．“月亮女神”的角速度小于“嫦娥一号”的角速度 |
| C．“月亮女神”的线速度小于“嫦娥一号”的线速度 |
| D．“月亮女神”的加速度小于“嫦娥一号”的加速度 |