题目内容
15. 三个电阻器按照如图所示的电路连接,其阻值之比为R1:R2:R3=1:3:6,则电路工作时,通过三个电阻器R1、R2、R3上的电流之比I1:I2:I3为( )
三个电阻器按照如图所示的电路连接,其阻值之比为R1:R2:R3=1:3:6,则电路工作时,通过三个电阻器R1、R2、R3上的电流之比I1:I2:I3为( )| A. | 6:3:1 | B. | 1:3:6 | C. | 6:2:1 | D. | 3:2:1 |
分析 明确电路结构,根据串并联电路中电流关系进行分析,即可明确电流之比
解答 解:R2与R3并联,两电阻中电流之比等于电阻的反比,则R2:R3=6:3=2:1;
R1电流等于R2和R3中电流之和,故电流之比应为3:2:1;
故选:D.
点评 本题考查串并联电路中的电流规律,要掌握并联电路中电流之比等于电阻的倒数之比.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
6. 如图所示,一个教学用的直角三角板的边长分别为a、b、c,被沿两直角边的细绳A、B悬吊在天花板上,且斜边c恰好平行天花板,过直角的竖直线为MN.设A、B两绳对三角形薄板的拉力分别为Fa和Fb,已知Fa和Fb及薄板的重力为在同一平面的共点力,则下列判断正确的是( )
如图所示,一个教学用的直角三角板的边长分别为a、b、c,被沿两直角边的细绳A、B悬吊在天花板上,且斜边c恰好平行天花板,过直角的竖直线为MN.设A、B两绳对三角形薄板的拉力分别为Fa和Fb,已知Fa和Fb及薄板的重力为在同一平面的共点力,则下列判断正确的是( )
 如图所示,一个教学用的直角三角板的边长分别为a、b、c,被沿两直角边的细绳A、B悬吊在天花板上,且斜边c恰好平行天花板,过直角的竖直线为MN.设A、B两绳对三角形薄板的拉力分别为Fa和Fb,已知Fa和Fb及薄板的重力为在同一平面的共点力,则下列判断正确的是( )
如图所示,一个教学用的直角三角板的边长分别为a、b、c,被沿两直角边的细绳A、B悬吊在天花板上,且斜边c恰好平行天花板,过直角的竖直线为MN.设A、B两绳对三角形薄板的拉力分别为Fa和Fb,已知Fa和Fb及薄板的重力为在同一平面的共点力,则下列判断正确的是( )| A. | 薄板的重心不在MN线上 | |
| B. | 薄板所受重力的反作用力的作用点在MN的延长线上 | |
| C. | 两绳对薄板的拉力Fa和Fb是由于薄板发生形变而产生 | |
| D. | 两绳对薄板的拉力Fa和Fb之比为Fa:Fb=b:a |
3. 如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法正确的是( )
如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法正确的是( )
 如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法正确的是( )
如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法正确的是( )| A. | 质点由O到达各点的时间之比ta:tb:tc:td=1:2:3:4 | |
| B. | 质点通过各点的速率之比va:vb:vc:vd=1:2:3:4 | |
| C. | 在斜面上od间运动的平均速度$\overline{v}$=vb | |
| D. | 在斜面上od间运动的平均速度$\overline{v}$=$\frac{{v}_{d}}{2}$ |
10. 如图所示,粗糙斜面的倾角为30°,轻绳通过两个滑轮与A相连,A与斜面间错摩擦因数为μ=$\frac{\sqrt{3}}{2}$轻绳的另一端固定于天花板上,不计轻绳与滑轮的摩擦.物块A的质量为m,不计滑轮的质量,挂上物块B后,当滑轮两边轻绳的夹角为90°时,A、B恰能保持静止,且A所受摩擦力向下,则物块B的质量为( )
如图所示,粗糙斜面的倾角为30°,轻绳通过两个滑轮与A相连,A与斜面间错摩擦因数为μ=$\frac{\sqrt{3}}{2}$轻绳的另一端固定于天花板上,不计轻绳与滑轮的摩擦.物块A的质量为m,不计滑轮的质量,挂上物块B后,当滑轮两边轻绳的夹角为90°时,A、B恰能保持静止,且A所受摩擦力向下,则物块B的质量为( )
 如图所示,粗糙斜面的倾角为30°,轻绳通过两个滑轮与A相连,A与斜面间错摩擦因数为μ=$\frac{\sqrt{3}}{2}$轻绳的另一端固定于天花板上,不计轻绳与滑轮的摩擦.物块A的质量为m,不计滑轮的质量,挂上物块B后,当滑轮两边轻绳的夹角为90°时,A、B恰能保持静止,且A所受摩擦力向下,则物块B的质量为( )
如图所示,粗糙斜面的倾角为30°,轻绳通过两个滑轮与A相连,A与斜面间错摩擦因数为μ=$\frac{\sqrt{3}}{2}$轻绳的另一端固定于天花板上,不计轻绳与滑轮的摩擦.物块A的质量为m,不计滑轮的质量,挂上物块B后,当滑轮两边轻绳的夹角为90°时,A、B恰能保持静止,且A所受摩擦力向下,则物块B的质量为( )| A. | $\frac{\sqrt{2}}{2}$m | B. | $\frac{5\sqrt{2}}{4}$m | C. | m | D. | 2m |
7.某实验小组要描绘一只规格为”2.5V,0.5A”小灯泡的伏安特性曲线,除了提供导线和开关外,还有以下一些器材:
A.电源E(电动势为3.0V,内阻不计)
B.电压表V(量程为0-3.0V,内阻约为2kΩ)
C.电流表A(量程为0-0.6A,内阻约为1Ω)
D.滑动变阻器R(最大阻值10Ω,额定电流1A)
(1)为完成本实验,请用笔画线当导线,将如图1实物图连成完整的电路,要求实验误差尽可能的小.(图中有几根导线已经接好)
(2)下表中的数据是该小组在实验中测得的,请根据表格中的数据在如图2方格纸上作出电珠的伏安特性曲线.根据I-U图象,由图分析可知,小灯泡电阻随温度T变化的关系是灯丝电阻随温度的升高而增大.

(3)若将本题中的小灯泡接在电动势是2.5V、内阻是5.0Ω的电池两端,则小灯泡的实际功率约为0.30W(保留两位有效数字).
A.电源E(电动势为3.0V,内阻不计)
B.电压表V(量程为0-3.0V,内阻约为2kΩ)
C.电流表A(量程为0-0.6A,内阻约为1Ω)
D.滑动变阻器R(最大阻值10Ω,额定电流1A)
(1)为完成本实验,请用笔画线当导线,将如图1实物图连成完整的电路,要求实验误差尽可能的小.(图中有几根导线已经接好)
(2)下表中的数据是该小组在实验中测得的,请根据表格中的数据在如图2方格纸上作出电珠的伏安特性曲线.根据I-U图象,由图分析可知,小灯泡电阻随温度T变化的关系是灯丝电阻随温度的升高而增大.
| U/V | 0.00 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 |
| I/A | 0.00 | 0.17 | 0.30 | 0.39 | 0.45 | 0.49 |

(3)若将本题中的小灯泡接在电动势是2.5V、内阻是5.0Ω的电池两端,则小灯泡的实际功率约为0.30W(保留两位有效数字).
4. 如图所示,用一恒力F通过一定滑轮拉动一箱子,箱子的质量为m,箱子与地面的动摩擦因 数为μ,某时刻绳与水平面的夹角为θ,绳端的速度为v,不计绳与滑轮的摩擦,重力加速度为g,则该时刻( )
如图所示,用一恒力F通过一定滑轮拉动一箱子,箱子的质量为m,箱子与地面的动摩擦因 数为μ,某时刻绳与水平面的夹角为θ,绳端的速度为v,不计绳与滑轮的摩擦,重力加速度为g,则该时刻( )
 如图所示,用一恒力F通过一定滑轮拉动一箱子,箱子的质量为m,箱子与地面的动摩擦因 数为μ,某时刻绳与水平面的夹角为θ,绳端的速度为v,不计绳与滑轮的摩擦,重力加速度为g,则该时刻( )
如图所示,用一恒力F通过一定滑轮拉动一箱子,箱子的质量为m,箱子与地面的动摩擦因 数为μ,某时刻绳与水平面的夹角为θ,绳端的速度为v,不计绳与滑轮的摩擦,重力加速度为g,则该时刻( )| A. | 箱子的速度大小为vcosθ | |
| B. | 箱子的速度大小为$\frac{v}{cosθ}$ | |
| C. | 箱子的加速度大小为$\frac{Fcosθ-μmg}{m}$ | |
| D. | 箱子的加速度大小为$\frac{F(cosθ+μsinθ)-μmg}{m}$ |
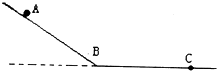 如图所示,物体由静止从A点沿斜面匀加速下滑,随后在水平面上作匀减速运动,最后停止于C点,已知AB=6m,BC=8m,整个运动历时12s,求物体在AB和BC运动的加速度和最大速度.
如图所示,物体由静止从A点沿斜面匀加速下滑,随后在水平面上作匀减速运动,最后停止于C点,已知AB=6m,BC=8m,整个运动历时12s,求物体在AB和BC运动的加速度和最大速度. 如图所示为6个质量均为m的人搭成的叠罗汉.若上面人的压力平均作用在下面的两个人肩上.求:
如图所示为6个质量均为m的人搭成的叠罗汉.若上面人的压力平均作用在下面的两个人肩上.求: 市场上有一种用两节干电池供电的小型电风扇.某物理研究小组想粗测电风扇正常运转时电能转化为机械能的效率.于是找到了一台该种电风扇并从铭牌上读出了额定电压U,但是其它字迹看不清楚.该研究小组成员打开电风扇底座上的电源盖并取出了两节电池,并从电风扇装电池处两端各接出一条引线,手边提供的器材有电流表,电压表,滑动变阻器,备用电池若干节,电键,若干导线,固定电池的电池盒.
市场上有一种用两节干电池供电的小型电风扇.某物理研究小组想粗测电风扇正常运转时电能转化为机械能的效率.于是找到了一台该种电风扇并从铭牌上读出了额定电压U,但是其它字迹看不清楚.该研究小组成员打开电风扇底座上的电源盖并取出了两节电池,并从电风扇装电池处两端各接出一条引线,手边提供的器材有电流表,电压表,滑动变阻器,备用电池若干节,电键,若干导线,固定电池的电池盒.