题目内容
10. 如图所示,粗糙斜面的倾角为30°,轻绳通过两个滑轮与A相连,A与斜面间错摩擦因数为μ=$\frac{\sqrt{3}}{2}$轻绳的另一端固定于天花板上,不计轻绳与滑轮的摩擦.物块A的质量为m,不计滑轮的质量,挂上物块B后,当滑轮两边轻绳的夹角为90°时,A、B恰能保持静止,且A所受摩擦力向下,则物块B的质量为( )
如图所示,粗糙斜面的倾角为30°,轻绳通过两个滑轮与A相连,A与斜面间错摩擦因数为μ=$\frac{\sqrt{3}}{2}$轻绳的另一端固定于天花板上,不计轻绳与滑轮的摩擦.物块A的质量为m,不计滑轮的质量,挂上物块B后,当滑轮两边轻绳的夹角为90°时,A、B恰能保持静止,且A所受摩擦力向下,则物块B的质量为( )| A. | $\frac{\sqrt{2}}{2}$m | B. | $\frac{5\sqrt{2}}{4}$m | C. | m | D. | 2m |
分析 A恰能保持静止且A所受摩擦力沿斜面向下,说明静摩擦力沿斜面向下,且达到最大值.先对A受力分析,运用共点力平衡条件和摩擦力公式求出细线的拉力;再对B受力分析,再次运用共点力平衡条件求出B的质量.
解答 解:先对A受力分析,如图
根据共点力平衡条件,有
mgsin30°+f=T
N=mgcos30°
又f=μN
联立解得,T=12.5m
再对B受力分析,设B的质量为M,则有$\sqrt{2}$T=Mg
联立解得:M=$\frac{5\sqrt{2}}{4}$m.
故选:B
点评 本题关键是先后对物体A、B受力分析,根据共点力平衡条件,结合合成法或正交分解法列式求解.

练习册系列答案
相关题目
18.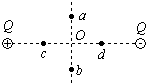 如图所示,两个等量异号的点电荷在其连线的中垂线上有与连线中点O等距离的两点a、b,在连线上有距中点O等距离的两点c、d,则下列场强大小关系式正确的是( )
如图所示,两个等量异号的点电荷在其连线的中垂线上有与连线中点O等距离的两点a、b,在连线上有距中点O等距离的两点c、d,则下列场强大小关系式正确的是( )
 如图所示,两个等量异号的点电荷在其连线的中垂线上有与连线中点O等距离的两点a、b,在连线上有距中点O等距离的两点c、d,则下列场强大小关系式正确的是( )
如图所示,两个等量异号的点电荷在其连线的中垂线上有与连线中点O等距离的两点a、b,在连线上有距中点O等距离的两点c、d,则下列场强大小关系式正确的是( )| A. | Ea=Eb<Ec | B. | Ea=Eo=Eb | C. | Φa=Φb>Φc | D. | φc>φO>φd |
5. 如图所示,两根足够长的直金属导轨平行放置在倾角为θ的绝缘斜面上,两导轨间距为L,底端接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直,导轨和杆ab的电阻可忽略.整个装置处于磁感应强度为B的匀强磁场中,磁场方向垂直斜面向上.让杆ab沿轨道由静止开始下滑,导轨和杆ab接触良好,不计它们之间的摩擦,杆ab由静止下滑距离S时,已处于匀速运动.重力加速度为g.则( )
如图所示,两根足够长的直金属导轨平行放置在倾角为θ的绝缘斜面上,两导轨间距为L,底端接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直,导轨和杆ab的电阻可忽略.整个装置处于磁感应强度为B的匀强磁场中,磁场方向垂直斜面向上.让杆ab沿轨道由静止开始下滑,导轨和杆ab接触良好,不计它们之间的摩擦,杆ab由静止下滑距离S时,已处于匀速运动.重力加速度为g.则( )
 如图所示,两根足够长的直金属导轨平行放置在倾角为θ的绝缘斜面上,两导轨间距为L,底端接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直,导轨和杆ab的电阻可忽略.整个装置处于磁感应强度为B的匀强磁场中,磁场方向垂直斜面向上.让杆ab沿轨道由静止开始下滑,导轨和杆ab接触良好,不计它们之间的摩擦,杆ab由静止下滑距离S时,已处于匀速运动.重力加速度为g.则( )
如图所示,两根足够长的直金属导轨平行放置在倾角为θ的绝缘斜面上,两导轨间距为L,底端接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直,导轨和杆ab的电阻可忽略.整个装置处于磁感应强度为B的匀强磁场中,磁场方向垂直斜面向上.让杆ab沿轨道由静止开始下滑,导轨和杆ab接触良好,不计它们之间的摩擦,杆ab由静止下滑距离S时,已处于匀速运动.重力加速度为g.则( )| A. | 匀速运动时杆ab的速度为$\frac{mgRsinθ}{{B}^{2}{L}^{2}}$ | |
| B. | 匀速运动时杆ab受到的安培力大小为mgsinθ | |
| C. | 杆ab由静止下滑距离S过程中,安培力做功为mgSsinθ | |
| D. | 杆ab由静止下滑距离S过程中,电阻R产生的热量为mgSsinθ |
15. 三个电阻器按照如图所示的电路连接,其阻值之比为R1:R2:R3=1:3:6,则电路工作时,通过三个电阻器R1、R2、R3上的电流之比I1:I2:I3为( )
三个电阻器按照如图所示的电路连接,其阻值之比为R1:R2:R3=1:3:6,则电路工作时,通过三个电阻器R1、R2、R3上的电流之比I1:I2:I3为( )
 三个电阻器按照如图所示的电路连接,其阻值之比为R1:R2:R3=1:3:6,则电路工作时,通过三个电阻器R1、R2、R3上的电流之比I1:I2:I3为( )
三个电阻器按照如图所示的电路连接,其阻值之比为R1:R2:R3=1:3:6,则电路工作时,通过三个电阻器R1、R2、R3上的电流之比I1:I2:I3为( )| A. | 6:3:1 | B. | 1:3:6 | C. | 6:2:1 | D. | 3:2:1 |
2.下列说法中,关于时间的是( )
| A. | 学校上午8点开始上第一节课,到8点45分下课 | |
| B. | 小学每节课只有40分钟 | |
| C. | 我走不动了,休息一下吧 | |
| D. | 邢慧娜获得雅典奥运会女子10000m冠军,成绩是30分24秒36 |
19.如图所示为某示波管内的聚焦电场,实线和虚线分别表示电场线和等势线.则( )


| A. | 场强Ea>Eb>Ec | |
| B. | 电势ϕa>ϕb,ϕc>ϕb | |
| C. | 沿cba路径移动质子与电子,电荷的电势能改变是一样的 | |
| D. | 沿bc方向直线射入的电子一定做直线运动 |
20.如图1为用打点计时器测定匀变速直线运动平均速度的实验时记录下的一条纸带.纸 带上选取1、2、3、4、5各点为计数点,将直尺靠在纸带边,零刻线与纸带上某一点0对齐.由0到1、2、3…点的距离分别用d1、d2、d3…表示(已知相邻计数点间还有4个计时点没画出),测量出d1、d2、d3…的值,已填入表中.已知打点计时器所用交流电的频率为50Hz,即每0.02秒打下一个计时点,以打O点时为计时起点,由测量数据计算出纸带上打下点2、4两点时小车的速度V,并在V-t图象上(图2)描绘出对应的图线.


| 距离 | d1 | d2 | d3 | d4 | d5 | d6 |
| 测量值(cm) | 1.30 | 2.40 | 3.30 | 4.00 | 4.50 | 4.85 |
| 瞬时速度(cm/s) | 12.00 | 8.00 | 4.25 |
