题目内容

6．如图所示，一个教学用的直角三角板的边长分别为a、b、c，被沿两直角边的细绳A、B悬吊在天花板上，且斜边c恰好平行天花板，过直角的竖直线为MN．设A、B两绳对三角形薄板的拉力分别为Fa和Fb，已知Fa和Fb及薄板的重力为在同一平面的共点力，则下列判断正确的是（　　）
A．薄板的重心不在MN线上
B．薄板所受重力的反作用力的作用点在MN的延长线上
C．两绳对薄板的拉力Fa和Fb是由于薄板发生形变而产生
D．两绳对薄板的拉力Fa和Fb之比为Fa：Fb=b：a

分析 根据三力汇交原理确定重心的位置，根据合力为零，运用合成法求出Fa和Fb的比值．

解答 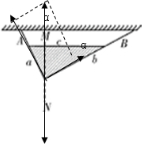解：A、三角形薄板受重力、两个拉力处于平衡，三个力虽然不是作用在同一点，但不平行，根据三力汇交原理，三个力的延长线必然交于一点，由几何关系，三个力一定交于三角形下面的顶点，所以重心一定在MN线上．故A错误．
B、重心一定在MN线上，则根据牛顿第三定律知，重力的反作用力的作用点在MN的延长线上，故B正确．
C、两绳对薄板的拉力Fa和Fb是由于绳发生形变而产生．故C错误．
D、三角形薄板受力分析如图，根据合力等于0，则Fa=mgcosα，Fb=mgsinα，则Fa：Fb=cotα=b：a．故D正确．
故选：BD

点评 解决本题的关键理解共点力，能够正确地进行受力分析，运用共点力平衡进行求解

练习册系列答案
相关题目
16．如图所示，线圈A接交流电源，其电流的表达式i=Imsin$\frac{2π}{T}$t，设交流电为正半周期时线圈A的上端电势高于下端电势，副线圈B接光滑导轨及光滑金属棒ab，导轨间的磁场方向如图．据此可知，在0-T时间内ab具有向右加速度的时间段是（　　）
A．0-$\frac{T}{4}$B．$\frac{T}{4}$-$\frac{T}{2}$C．$\frac{T}{2}$-$\frac{3T}{4}$D．$\frac{3T}{4}$-T
17．如图所示，A为粗糙长木板在光滑水平面上向右滑行，B为小木块在A上向右滑行，某时刻A的速度为v1，B的速度为v2，关于A、B之间的摩擦力下列说法正确的是（　　）
A．若v1＞v2，A给B向左的滑动摩擦力B．若v1＞v2，B给A向右的滑动摩擦力
C．若v1＜v2，A受到向右的滑动摩擦力D．若v1＜v2，B受到向右的滑动摩擦力
14．在火箭竖直向上加速运动的过程中，宇航员对其座椅的压力（　　）宇航员的重力．
A．大于B．小于
1．汽车在水平路面上转弯时，转弯时如果速度过大，会出现（　　）现象．
A．离心B．向心
11．如图所示，abcd为水平放置的平行线“匸”形光滑金属导轨，间距为l，导轨间有垂直于导轨平面的匀强磁场，磁感应强度大小为B，导轨电阻不计．已知金属杆MN倾斜放置，与导轨成θ角，单位长度的电阻为r，保持金属杆以速度v沿平行于cd的方向滑动（金属杆滑动过程中与导轨接触良好）．则（　　）
A．电路中感应电动势为Blv
B．电路中感应电流的大小为$\frac{Bvsinθ}{r}$
C．金属杆所受安培力的大小为$\frac{{{B^2}lvsinθ}}{r}$
D．金属杆的热功率为$\frac{{{B^2}l{v^2}}}{rsinθ}$
18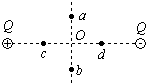．如图所示，两个等量异号的点电荷在其连线的中垂线上有与连线中点O等距离的两点a、b，在连线上有距中点O等距离的两点c、d，则下列场强大小关系式正确的是（　　）
A．Ea=Eb＜EcB．Ea=Eo=EbC．Φa=Φb＞ΦcD．φc＞φO＞φd
15．三个电阻器按照如图所示的电路连接，其阻值之比为R1：R2：R3=1：3：6，则电路工作时，通过三个电阻器R1、R2、R3上的电流之比I1：I2：I3为（　　）
A．6：3：1B．1：3：6C．6：2：1D．3：2：1
16．若实验中，算出各点的时刻所对应的瞬时速度，计算加速度最合理的方法是（　　）
A．根据实验数据画出图出v-t图，量出倾斜角α，由a=tanα，求出加速度
B．根据实验数据正确画出v-t图，由图线上的一点对应的坐标（t，v），a=$\frac{V}{t}$
C．根据实验数据正确画出v--t图，由图线上距离较大的两点对应的坐标（t，v），按求斜率的方法计算出加速度
D．根据实验数据正确画出v-t图，由图线上距离较近的两点对应的坐标（t，v），按求斜率的方法计算出加速度

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网