Question

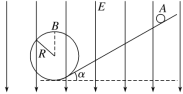
【题目】如图所示，竖直面内的光滑绝缘轨道，处于竖直向下的匀强电场中．一个带负电的小球从斜轨道上的A点由静止释放，沿轨道滑下，已知小球的质量为m，电荷量为－q，匀强电场的场强大小为E，斜轨道的倾角为α，圆轨道半径为R，斜轨道与圆轨道平滑连接，小球的重力大于所受的电场力．

(1) 求小球沿轨道滑下的加速度的大小；

(2) 若使小球通过圆轨道顶端的B点，求A点距圆轨道最低点的竖直高度h1至少为多大；

(3) 若小球从距圆轨道最低点的竖直高度h2＝5R处由静止释放，假设其能通过圆轨道顶端B点，求从释放到B点的过程中小球机械能的改变量．

Answer 1

【答案】（1）（2）R（3）减少3qER.

【解析】

(1)由牛顿第二定律有

(mg－qE)sinα＝ma

解得

a＝

(2)球恰能过B点有：

mg－qE＝m①

由动能定理，从A点到B点过程，则有：

②

由①②解得

h1＝R.

(3)从释放到B的过程中，因电场力做的总功为负功，电势能增加，则增加量：

ΔE＝qE(h2－2R)＝qE(5R－2R)＝3qER.

由能量守恒定律得机械能减少，且减少量为3qER.

答案：（1）（2）R（3）减少3qER.