题目内容
如图,在xoy平面内,MN和x轴之间有平行于y轴的匀强电场,方向向下,在 xoy平面的第一象限内有垂直向里的匀强磁场.y轴上离坐标原点4L的A点处有一电子枪,可以沿+x方向射出速度为v0的电子(质量为m,电量为e).如果电场和磁场同时存在,电子将做匀速直线运动,不计重力的影响.
(1)如果撤去电场,只保留磁场,电子将从x轴上距坐标原点3L的C点离开磁场.求磁感应强度B和电场强度E的大小各多大.
(2)如果撤去磁场,只保留电场,电子将从D离开电场.求D点的横坐标.
(3)如果撤去电场,只保留磁场,电子速度变为V,求电子在磁场中的运动时间.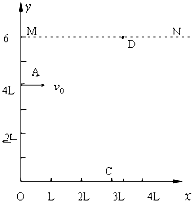
(1)如果撤去电场,只保留磁场,电子将从x轴上距坐标原点3L的C点离开磁场.求磁感应强度B和电场强度E的大小各多大.
(2)如果撤去磁场,只保留电场,电子将从D离开电场.求D点的横坐标.
(3)如果撤去电场,只保留磁场,电子速度变为V,求电子在磁场中的运动时间.

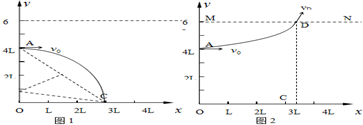
(1)只有磁场时,电子运动轨迹如图1所示
洛伦兹力提供向心力 Bev0=m
| ||
| R |
由几何关系 R2=(3L)2+(4L-R)2
解得:B=
| 8mv0 |
| 25eL |
电子做匀速直线运动 Ee=Bev0
解得:E=
8m
| ||
| 25eL |
(2)只有电场时,电子从MN上的D点离开电场,如图2所示
设D点横坐标为x x=v0t
2L=
| 1 |
| 2 |
| eE |
| m |
求出D点的横坐标为x=
5
| ||
| 2 |
(3)分四种情况
转动周期为:T=
| 2πm |
| eB |
| mv |
| eB |
①当半径r≤2L,速度v≤
| 2eBL |
| m |
运动时间为半个周期,
t1=
| T |
| 2 |
| πm |
| eB |
| 25πL |
| 8v0 |
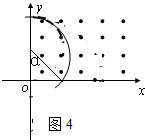
②当半径2L<r<4L,电子速度
| 2eBL |
| m |
| 4eBL |
| m |
圆心角为θ1=π-α,由几何关系知:cosα=
| 4L-r |
| r |
| 4eBL |
| mv |
所以,运动时间为:t2=
| π-α |
| 2π |
| 25L |
| 8v0 |
| 32v0 |
| 25v |
③当r=4L时,速度v=
| 4eBL |
| m |
如图5,运动时间为四分之一个周期,t3=
| T |
| 4 |
| πm |
| 2eB |
| 25πL |
| 16v0 |
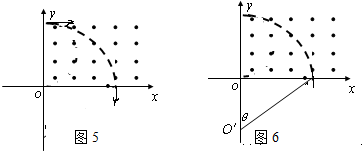
④当r>4L时,速度v>
| 4eBL |
| m |
设此时的圆心为O′在坐标原点之下,由图可知,圆心角为θ2,cosθ2=
| OO′ |
| r |
| r-4L |
| r |
| 4eBL |
| mv |
所以,运动时间为:t4=
| θ2 |
| 2π |
| 25L |
| 8v0 |
| 32v0 |
| 25v |
答:(1)如果撤去电场,只保留磁场,电子将从x轴上距坐标原点3L的C点离开磁场.求磁感应强度
| 8mv0 |
| 25eL |
8m
| ||
| 25eL |
(2)如果撤去磁场,只保留电场,电子将从D离开电场.则D点的横坐标3.5L.
(3)如果撤去电场,只保留磁场,电子速度变为V,则电子在磁场中的运动时间如上时间表述.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013?厦门模拟)如图,在xOy平面内有一列沿x轴正方向传播的简谐横波,振幅为0.1m,频率为2.5Hz.在t=0时,平衡位置坐标x=2m的质点P点正经过平衡位置向下,平衡位置坐标x=5m的质点Q点位于波谷,且PQ之间只有一波峰,则下列说法正确的是( )
(2013?厦门模拟)如图,在xOy平面内有一列沿x轴正方向传播的简谐横波,振幅为0.1m,频率为2.5Hz.在t=0时,平衡位置坐标x=2m的质点P点正经过平衡位置向下,平衡位置坐标x=5m的质点Q点位于波谷,且PQ之间只有一波峰,则下列说法正确的是( ) (2011?开封二模)如图,在xoy平面内,直线MON与x轴成45°夹角.在MON左侧且x<0的空间存在着沿x轴负方向的匀强电场,场强大小为E=10V/m;在MON的右侧空间存在着垂直直面向里的匀强磁场;在MON左侧且x>0的空间既无磁场也无电场;一个重力不计的带负电的粒子从坐标原点O以大小为V0=200m/s的速度沿着y轴负方向进入匀强磁场.已知粒子的比荷为q/m=103C/kg,粒子从O点离开后,第二次经过y轴时从y轴上A点,恰好与y轴正方向成45°角射出电场,试求:
(2011?开封二模)如图,在xoy平面内,直线MON与x轴成45°夹角.在MON左侧且x<0的空间存在着沿x轴负方向的匀强电场,场强大小为E=10V/m;在MON的右侧空间存在着垂直直面向里的匀强磁场;在MON左侧且x>0的空间既无磁场也无电场;一个重力不计的带负电的粒子从坐标原点O以大小为V0=200m/s的速度沿着y轴负方向进入匀强磁场.已知粒子的比荷为q/m=103C/kg,粒子从O点离开后,第二次经过y轴时从y轴上A点,恰好与y轴正方向成45°角射出电场,试求: (2013?闵行区二模)如图,在xOy平面内有一列沿x轴传播的简谐横波,频率为2.5Hz.在t=0时,P点位于平衡位置,且速度方向向下,Q点位于平衡位置下方的最大位移处.则在t=0.35s时,P、Q两质点的( )
(2013?闵行区二模)如图,在xOy平面内有一列沿x轴传播的简谐横波,频率为2.5Hz.在t=0时,P点位于平衡位置,且速度方向向下,Q点位于平衡位置下方的最大位移处.则在t=0.35s时,P、Q两质点的( ) (2012?珠海一模)如图,在xoy平面内,MN和x轴之间有平行于y轴的匀强电场,方向向下,在 xoy平面的第一象限内有垂直向里的匀强磁场.y轴上离坐标原点4L的A点处有一电子枪,可以沿+x方向射出速度为v0的电子(质量为m,电量为e).如果电场和磁场同时存在,电子将做匀速直线运动,不计重力的影响.
(2012?珠海一模)如图,在xoy平面内,MN和x轴之间有平行于y轴的匀强电场,方向向下,在 xoy平面的第一象限内有垂直向里的匀强磁场.y轴上离坐标原点4L的A点处有一电子枪,可以沿+x方向射出速度为v0的电子(质量为m,电量为e).如果电场和磁场同时存在,电子将做匀速直线运动,不计重力的影响. 如图,在xoy平面内第二象限-10cm≤x≤0区域内有垂直纸面向内的匀强磁场B,其大小为0.2T,在A(-6cm,0)点有一粒子发射源,向x轴上方180°范围内发射v=2.0×107m/s的负粒子,粒子的比荷为2.0×109C/kg,不计粒子重力,求:
如图,在xoy平面内第二象限-10cm≤x≤0区域内有垂直纸面向内的匀强磁场B,其大小为0.2T,在A(-6cm,0)点有一粒子发射源,向x轴上方180°范围内发射v=2.0×107m/s的负粒子,粒子的比荷为2.0×109C/kg,不计粒子重力,求: