题目内容
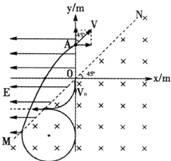
 (2011?开封二模)如图,在xoy平面内,直线MON与x轴成45°夹角.在MON左侧且x<0的空间存在着沿x轴负方向的匀强电场,场强大小为E=10V/m;在MON的右侧空间存在着垂直直面向里的匀强磁场;在MON左侧且x>0的空间既无磁场也无电场;一个重力不计的带负电的粒子从坐标原点O以大小为V0=200m/s的速度沿着y轴负方向进入匀强磁场.已知粒子的比荷为q/m=103C/kg,粒子从O点离开后,第二次经过y轴时从y轴上A点,恰好与y轴正方向成45°角射出电场,试求:
(2011?开封二模)如图,在xoy平面内,直线MON与x轴成45°夹角.在MON左侧且x<0的空间存在着沿x轴负方向的匀强电场,场强大小为E=10V/m;在MON的右侧空间存在着垂直直面向里的匀强磁场;在MON左侧且x>0的空间既无磁场也无电场;一个重力不计的带负电的粒子从坐标原点O以大小为V0=200m/s的速度沿着y轴负方向进入匀强磁场.已知粒子的比荷为q/m=103C/kg,粒子从O点离开后,第二次经过y轴时从y轴上A点,恰好与y轴正方向成45°角射出电场,试求:(1)带点粒子第一次经过MON直线时速度的大小和方向;
(2)磁感应强度B的大小;
(3)A点的坐标.
分析:(1)洛仑兹力永不做功,故粒子的速度不变;因粒子从同一条直线上进入和离开时角度相同,则可知粒子离开磁场的方向;
(2)粒子进入电场后做减速运动,最后以相同的速度进入磁场做匀速圆周运动,向下偏转;第二次进入磁场后向下偏转后再次进入磁场做类平抛运动,最后从A点离开;由类平抛运动的规律可得出粒子的半径,由洛仑兹力充当向心力可得出磁感应强度;
(3)粒子横坐标为零,根据类平抛知识求出竖直高度即可求出A点坐标.
(2)粒子进入电场后做减速运动,最后以相同的速度进入磁场做匀速圆周运动,向下偏转;第二次进入磁场后向下偏转后再次进入磁场做类平抛运动,最后从A点离开;由类平抛运动的规律可得出粒子的半径,由洛仑兹力充当向心力可得出磁感应强度;
(3)粒子横坐标为零,根据类平抛知识求出竖直高度即可求出A点坐标.
解答:解:(1)粒子进入磁场后,只受洛仑兹力做匀速圆周运动,所以粒子第一次经过MON直线时,速度大小不变为v0,由对称性可知方向沿x负方向;
(2)因为A点的速度与y轴成45°,所以vx=vy;
粒子在电场中只受沿x轴正向的电场力,y方向上不受力,故有:vy=v0,vx=vy=v0
粒子第二次进入电场做类平抛运动,在x轴方向水平位移为R,则有
vx2=2a×2R=
解得:R=
=1m
在磁场中,由Bqv0=m
得:
B=
=0.2T;
(3)粒子在电场中做平抛运动,由图可知:
在y轴方向2R+y=v0t
在x轴方向2R=
t
因vx=vy=v0
所以y=2R=2m
则A点的坐标为(0,2)
(2)因为A点的速度与y轴成45°,所以vx=vy;
粒子在电场中只受沿x轴正向的电场力,y方向上不受力,故有:vy=v0,vx=vy=v0
粒子第二次进入电场做类平抛运动,在x轴方向水平位移为R,则有
vx2=2a×2R=
| 4qER |
| m |
解得:R=
| mv2 |
| 4qE |
在磁场中,由Bqv0=m
| ||
| R |
B=
| mv0 |
| qR |
(3)粒子在电场中做平抛运动,由图可知:
在y轴方向2R+y=v0t
在x轴方向2R=
| vx |
| 2 |
因vx=vy=v0
所以y=2R=2m
则A点的坐标为(0,2)

点评:本题中粒子先在磁场中做圆周运动,后进入电场做直线运动,再次进和磁场后做圆周运动,离开后进入磁场做类平抛运动;过程较为复杂,在解题时要注意作出运动轨迹图,根据几何关系确定圆的圆心及半径;并注意类平抛及圆周运动间的关系.

练习册系列答案
相关题目
 (2011?开封二模)质量为m的汽车在平直路面上启动,启动过程的速度图象如图所示.从t1时刻起牵引力的功率保持不变,整个运动过程中汽车所受阻力恒为Ff,则( )
(2011?开封二模)质量为m的汽车在平直路面上启动,启动过程的速度图象如图所示.从t1时刻起牵引力的功率保持不变,整个运动过程中汽车所受阻力恒为Ff,则( ) (2011?开封二模)如图所示,物体原来静止在水平面上,用以水平力F拉物体,在F从0开始逐渐增大的过程中,物体先静止然后又做变加速运动,其加速度a随着外力F变化的图象如图所示,根据图中所标出的数据可以计算出( ) (g=10m/s2)
(2011?开封二模)如图所示,物体原来静止在水平面上,用以水平力F拉物体,在F从0开始逐渐增大的过程中,物体先静止然后又做变加速运动,其加速度a随着外力F变化的图象如图所示,根据图中所标出的数据可以计算出( ) (g=10m/s2) (2011?开封二模)水平路面上匀速运动的下车支架上有三个完全相同的小球ABC,当小车遇到障碍物D时,立即停下来,三个小球同时从支架上抛出,落到水平面上.已知三个小球的高度差相等,即hA-hB=hB-hC,下列说法中正确的是( )
(2011?开封二模)水平路面上匀速运动的下车支架上有三个完全相同的小球ABC,当小车遇到障碍物D时,立即停下来,三个小球同时从支架上抛出,落到水平面上.已知三个小球的高度差相等,即hA-hB=hB-hC,下列说法中正确的是( )