题目内容
 (2012?珠海一模)如图,在xoy平面内,MN和x轴之间有平行于y轴的匀强电场,方向向下,在 xoy平面的第一象限内有垂直向里的匀强磁场.y轴上离坐标原点4L的A点处有一电子枪,可以沿+x方向射出速度为v0的电子(质量为m,电量为e).如果电场和磁场同时存在,电子将做匀速直线运动,不计重力的影响.
(2012?珠海一模)如图,在xoy平面内,MN和x轴之间有平行于y轴的匀强电场,方向向下,在 xoy平面的第一象限内有垂直向里的匀强磁场.y轴上离坐标原点4L的A点处有一电子枪,可以沿+x方向射出速度为v0的电子(质量为m,电量为e).如果电场和磁场同时存在,电子将做匀速直线运动,不计重力的影响.(1)如果撤去电场,只保留磁场,电子将从x轴上距坐标原点3L的C点离开磁场.求磁感应强度B和电场强度E的大小各多大.
(2)如果撤去磁场,只保留电场,电子将从D离开电场.求D点的横坐标.
(3)如果撤去电场,只保留磁场,电子速度变为V,求电子在磁场中的运动时间.
分析:(1)电子在洛伦兹力作用下,做匀速圆周运动,根据牛顿第二定律与几何关系相结合,从而即可求解;再由电子电场力与洛伦兹力相平衡,即可求解;
(2)电子在电场中做类平抛运动,根据牛顿第二定律与运动学公式相结合,即可求解;
(3)分四种情况,根据转动周期与运动轨迹的半径,及几何关系相结合综合求出四种情况下的时间.
(2)电子在电场中做类平抛运动,根据牛顿第二定律与运动学公式相结合,即可求解;
(3)分四种情况,根据转动周期与运动轨迹的半径,及几何关系相结合综合求出四种情况下的时间.
解答: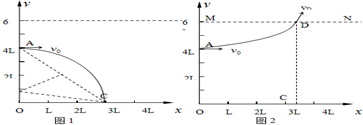 解:(1)只有磁场时,电子运动轨迹如图1所示
解:(1)只有磁场时,电子运动轨迹如图1所示
洛伦兹力提供向心力 Bev0=m
由几何关系 R2=(3L)2+(4L-R)2
解得:B=
电子做匀速直线运动 Ee=Bev0
解得:E=
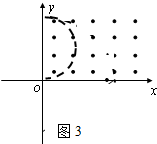
(2)只有电场时,电子从MN上的D点离开电场,如图2所示
设D点横坐标为x x=v0t
2L=
t2
求出D点的横坐标为x=
L≈3.5L
(3)分四种情况
转动周期为:T=
,半径为:r=
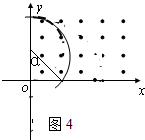
①当半径r≤2L,速度v≤
时,电子将从y轴上的某点离开磁场,如图3,
运动时间为半个周期,
t1=
=
=
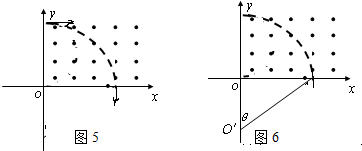
②当半径2L<r<4L,电子速度
<v<
时,电子将从x轴上某点离开磁场.如图4.
圆心角为θ1=π-α,由几何关系知:cosα=
=
-1
所以,运动时间为:t2=
T=
(π-arccos(
-1))
③当r=4L时,速度v=
,电子将垂直x轴离开磁场.
如图5,运动时间为四分之一个周期,t3=
=
=
④当r>4L时,速度v>
,电子将从x轴上某点离开磁场.如图6.
设此时的圆心为O′在坐标原点之下,由图可知,圆心角为θ2,cosθ2=
=
=1-
所以,运动时间为:t4=
?T=
arccos(1-
)
答:(1)如果撤去电场,只保留磁场,电子将从x轴上距坐标原点3L的C点离开磁场.求磁感应强度
和电场强度E的大小
.
(2)如果撤去磁场,只保留电场,电子将从D离开电场.则D点的横坐标3.5L.
(3)如果撤去电场,只保留磁场,电子速度变为V,则电子在磁场中的运动时间如上时间表述.
 解:(1)只有磁场时,电子运动轨迹如图1所示
解:(1)只有磁场时,电子运动轨迹如图1所示洛伦兹力提供向心力 Bev0=m
| ||
| R |
由几何关系 R2=(3L)2+(4L-R)2
解得:B=
| 8mv0 |
| 25eL |
电子做匀速直线运动 Ee=Bev0
解得:E=
8m
| ||
| 25eL |

(2)只有电场时,电子从MN上的D点离开电场,如图2所示
设D点横坐标为x x=v0t
2L=
| 1 |
| 2 |
| eE |
| m |
求出D点的横坐标为x=
5
| ||
| 2 |
(3)分四种情况
转动周期为:T=
| 2πm |
| eB |
| mv |
| eB |
①当半径r≤2L,速度v≤
| 2eBL |
| m |
运动时间为半个周期,
t1=
| T |
| 2 |
| πm |
| eB |
| 25πL |
| 8v0 |

②当半径2L<r<4L,电子速度
| 2eBL |
| m |
| 4eBL |
| m |
圆心角为θ1=π-α,由几何关系知:cosα=
| 4L-r |
| r |
| 4eBL |
| mv |
所以,运动时间为:t2=
| π-α |
| 2π |
| 25L |
| 8v0 |
| 32v0 |
| 25v |
③当r=4L时,速度v=
| 4eBL |
| m |
如图5,运动时间为四分之一个周期,t3=
| T |
| 4 |
| πm |
| 2eB |
| 25πL |
| 16v0 |

④当r>4L时,速度v>
| 4eBL |
| m |
设此时的圆心为O′在坐标原点之下,由图可知,圆心角为θ2,cosθ2=
| OO′ |
| r |
| r-4L |
| r |
| 4eBL |
| mv |
所以,运动时间为:t4=
| θ2 |
| 2π |
| 25L |
| 8v0 |
| 32v0 |
| 25v |
答:(1)如果撤去电场,只保留磁场,电子将从x轴上距坐标原点3L的C点离开磁场.求磁感应强度
| 8mv0 |
| 25eL |
8m
| ||
| 25eL |
(2)如果撤去磁场,只保留电场,电子将从D离开电场.则D点的横坐标3.5L.
(3)如果撤去电场,只保留磁场,电子速度变为V,则电子在磁场中的运动时间如上时间表述.
点评:考查带电粒子在电场与磁场中运动,结合受力来确定运动轨迹,除掌握必要的解题方法外,还要正确作出运动轨迹图,以及几何关系的确定.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 (2012?珠海一模)如图所示,质量为m的木块在质量为M的木板上滑行,木板与地面间动摩擦因数为μ1,木块与木板间的动摩擦因数为μ2,木板一直静止,那么木板受地面的摩擦力大小为( )
(2012?珠海一模)如图所示,质量为m的木块在质量为M的木板上滑行,木板与地面间动摩擦因数为μ1,木块与木板间的动摩擦因数为μ2,木板一直静止,那么木板受地面的摩擦力大小为( ) (2012?珠海一模)如图所示,图中的四个电表均为理想电表,当滑线变阻器滑动触点P向右端移动时,下面说法中正确是( )
(2012?珠海一模)如图所示,图中的四个电表均为理想电表,当滑线变阻器滑动触点P向右端移动时,下面说法中正确是( )