题目内容
 如图,在xoy平面内第二象限-10cm≤x≤0区域内有垂直纸面向内的匀强磁场B,其大小为0.2T,在A(-6cm,0)点有一粒子发射源,向x轴上方180°范围内发射v=2.0×107m/s的负粒子,粒子的比荷为2.0×109C/kg,不计粒子重力,求:
如图,在xoy平面内第二象限-10cm≤x≤0区域内有垂直纸面向内的匀强磁场B,其大小为0.2T,在A(-6cm,0)点有一粒子发射源,向x轴上方180°范围内发射v=2.0×107m/s的负粒子,粒子的比荷为2.0×109C/kg,不计粒子重力,求:(1)粒子在磁场中做圆周运动的半径.
(2)粒子在磁场中运动的最长时间是多少?
(3)若在0≤x≤10cm范围内加一与y轴平行向下的匀强电场,从y轴最上方飞出的粒子经过电场后恰好沿x轴正向从右边界飞出,试求出射点的坐标.
分析:(1)带电粒子在磁场中做圆周运动的向心力由洛伦兹力提供,写出动力学方程,即可求得粒子运动的半径;
(2)先求出周期,然后根据
=
求出粒子在磁场中运动的最长时间;
(3)粒子在电场中做类斜上抛运动,由于粒子经过电场后恰好沿x轴正向从右边界飞出,也可反向研究其运动的过程;
(2)先求出周期,然后根据
| t |
| T |
| θ |
| 2π |
(3)粒子在电场中做类斜上抛运动,由于粒子经过电场后恰好沿x轴正向从右边界飞出,也可反向研究其运动的过程;
解答:解:(1)带电粒子在磁场中做圆周运动的向心力由洛伦兹力提供
qvB=
得r=
=0.05m
(2)粒子在磁场中运动周期T=
=
×10-8s
如图所示的运动轨迹,运动时间最长为t
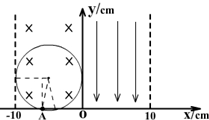
分析可得t=
T
即粒子在磁场中运动的最长时间为t=
(
+arcsin
)×10-8s
(3)从y轴最上方飞出的粒子坐标为(0,y3),右边界出射点为(10cm,y4)
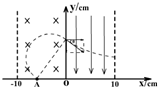
则有(2r)2=62+
得y3=8cm
sinθ=
有θ=37°
在x方向匀速直线运动 得t=
在y方向vy=vsin37° 出射时方向水平,则
′=0
△y=
?t=3.75cm
则y4=y3-△y=4.25cm
从电场右边界飞出的粒子坐标为(10cm,4.25cm)
答:(1)粒子在磁场中做圆周运动的半径为0.05m.
(2)粒子在磁场中运动的最长时间是t=
(
+arcsin
)×10-8;
(3)出射点的坐标为(10cm,4.25cm).
qvB=
| mv2 |
| r |
| mv |
| qB |
(2)粒子在磁场中运动周期T=
| 2πr |
| v |
| π |
| 2 |
如图所示的运动轨迹,运动时间最长为t

分析可得t=
π+2arcsin
| ||||
| 2π |
即粒子在磁场中运动的最长时间为t=
| 1 |
| 2 |
| π |
| 2 |
2
| ||
| 5 |
(3)从y轴最上方飞出的粒子坐标为(0,y3),右边界出射点为(10cm,y4)

则有(2r)2=62+
| y | 2 3 |
sinθ=
| 6 |
| 10 |
在x方向匀速直线运动 得t=
| 0.1 |
| vx |
在y方向vy=vsin37° 出射时方向水平,则
| v | y |
△y=
| vy |
| 2 |
则y4=y3-△y=4.25cm
从电场右边界飞出的粒子坐标为(10cm,4.25cm)
答:(1)粒子在磁场中做圆周运动的半径为0.05m.
(2)粒子在磁场中运动的最长时间是t=
| 1 |
| 2 |
| π |
| 2 |
2
| ||
| 5 |
(3)出射点的坐标为(10cm,4.25cm).
点评:本题是带电粒子在组合场中运动的问题,要求同学们能正确分析粒子的受力情况确定运动情况,结合几何关系以及半径公式、周期公式求解,难度比较大.

练习册系列答案
相关题目
 (2013?厦门模拟)如图,在xOy平面内有一列沿x轴正方向传播的简谐横波,振幅为0.1m,频率为2.5Hz.在t=0时,平衡位置坐标x=2m的质点P点正经过平衡位置向下,平衡位置坐标x=5m的质点Q点位于波谷,且PQ之间只有一波峰,则下列说法正确的是( )
(2013?厦门模拟)如图,在xOy平面内有一列沿x轴正方向传播的简谐横波,振幅为0.1m,频率为2.5Hz.在t=0时,平衡位置坐标x=2m的质点P点正经过平衡位置向下,平衡位置坐标x=5m的质点Q点位于波谷,且PQ之间只有一波峰,则下列说法正确的是( ) (2011?开封二模)如图,在xoy平面内,直线MON与x轴成45°夹角.在MON左侧且x<0的空间存在着沿x轴负方向的匀强电场,场强大小为E=10V/m;在MON的右侧空间存在着垂直直面向里的匀强磁场;在MON左侧且x>0的空间既无磁场也无电场;一个重力不计的带负电的粒子从坐标原点O以大小为V0=200m/s的速度沿着y轴负方向进入匀强磁场.已知粒子的比荷为q/m=103C/kg,粒子从O点离开后,第二次经过y轴时从y轴上A点,恰好与y轴正方向成45°角射出电场,试求:
(2011?开封二模)如图,在xoy平面内,直线MON与x轴成45°夹角.在MON左侧且x<0的空间存在着沿x轴负方向的匀强电场,场强大小为E=10V/m;在MON的右侧空间存在着垂直直面向里的匀强磁场;在MON左侧且x>0的空间既无磁场也无电场;一个重力不计的带负电的粒子从坐标原点O以大小为V0=200m/s的速度沿着y轴负方向进入匀强磁场.已知粒子的比荷为q/m=103C/kg,粒子从O点离开后,第二次经过y轴时从y轴上A点,恰好与y轴正方向成45°角射出电场,试求: (2013?闵行区二模)如图,在xOy平面内有一列沿x轴传播的简谐横波,频率为2.5Hz.在t=0时,P点位于平衡位置,且速度方向向下,Q点位于平衡位置下方的最大位移处.则在t=0.35s时,P、Q两质点的( )
(2013?闵行区二模)如图,在xOy平面内有一列沿x轴传播的简谐横波,频率为2.5Hz.在t=0时,P点位于平衡位置,且速度方向向下,Q点位于平衡位置下方的最大位移处.则在t=0.35s时,P、Q两质点的( ) (2012?珠海一模)如图,在xoy平面内,MN和x轴之间有平行于y轴的匀强电场,方向向下,在 xoy平面的第一象限内有垂直向里的匀强磁场.y轴上离坐标原点4L的A点处有一电子枪,可以沿+x方向射出速度为v0的电子(质量为m,电量为e).如果电场和磁场同时存在,电子将做匀速直线运动,不计重力的影响.
(2012?珠海一模)如图,在xoy平面内,MN和x轴之间有平行于y轴的匀强电场,方向向下,在 xoy平面的第一象限内有垂直向里的匀强磁场.y轴上离坐标原点4L的A点处有一电子枪,可以沿+x方向射出速度为v0的电子(质量为m,电量为e).如果电场和磁场同时存在,电子将做匀速直线运动,不计重力的影响.