题目内容
7.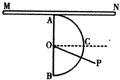 如图,ABC为某半圆形透明介质与空气的分界面,其圆心为O,直径为d.MN为紧靠A点并与直径AB垂直放置的足够长光屏,调节激光器,使PO光线从透明介质右侧弧面沿某一半径方向射向圆心O,当光线PO在O点的入射角为θ时,发现光屏MN的左右两侧均出现亮点,且左、右两侧亮点到A点的距离分别为$\frac{d}{2}$、$\frac{\sqrt{3}d}{2}$,则由以上信息可知( )
如图,ABC为某半圆形透明介质与空气的分界面,其圆心为O,直径为d.MN为紧靠A点并与直径AB垂直放置的足够长光屏,调节激光器,使PO光线从透明介质右侧弧面沿某一半径方向射向圆心O,当光线PO在O点的入射角为θ时,发现光屏MN的左右两侧均出现亮点,且左、右两侧亮点到A点的距离分别为$\frac{d}{2}$、$\frac{\sqrt{3}d}{2}$,则由以上信息可知( )| A. | θ=60° | |
| B. | 该透明介质的折射率n=$\sqrt{3}$ | |
| C. | 若增大θ,光屏MN上左侧亮点可能消失 | |
| D. | 若θ=45°,光屏MN上左、右两侧亮点到A点的距离相等 |
分析 作出光路图,由几何知识求出θ和折射角r,再由折射定律求折射率n.若增大θ,光线可能发生全反射,光屏MN上左侧亮点可能消失.
解答  解:A、作出光路图如图所示,由几何知识得:
解:A、作出光路图如图所示,由几何知识得:
tanθ=$\frac{\frac{1}{2}d}{\frac{\sqrt{3}}{2}d}$=$\frac{\sqrt{3}}{3}$,得 θ=30°,故A错误.
B、设折射角为r,则 tanr=$\frac{\frac{1}{2}d}{\frac{1}{2}d}$=1,r=45°
故折射率为 n=$\frac{sinr}{sinθ}$=$\sqrt{2}$,故B错误.
C、若增大θ,光线可能发生全反射,光屏MN上左侧亮点可能消失.故C正确.
D、若θ=45°,由反射定律和几何关系知,右侧亮点到A点的距离为$\frac{1}{2}$d.
由n=$\frac{sinr}{sinθ}$得 r=90°,光线恰好发生全反射,左侧亮点到A点的距离为0,故D错误.
故选:C.
点评 本题考查了光的折射定律,关键作出光路图,结合折射定律、全反射的条件和几何知识进行求解.

练习册系列答案
相关题目
7.一个半径是地球半径的2倍,质量是地球的36倍的行星,它表面的重力加速度是地球表面的加速度的( )
| A. | 6倍 | B. | 9倍 | C. | 4倍 | D. | 13.5倍 |
18.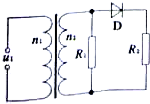 如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=22:5,原线圈接u1=220$\sqrt{2}$sin100πt(V)的交流电,电阻R1=R2=25Ω,D为理想二极管,则下列说法不正确的是( )
如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=22:5,原线圈接u1=220$\sqrt{2}$sin100πt(V)的交流电,电阻R1=R2=25Ω,D为理想二极管,则下列说法不正确的是( )
 如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=22:5,原线圈接u1=220$\sqrt{2}$sin100πt(V)的交流电,电阻R1=R2=25Ω,D为理想二极管,则下列说法不正确的是( )
如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=22:5,原线圈接u1=220$\sqrt{2}$sin100πt(V)的交流电,电阻R1=R2=25Ω,D为理想二极管,则下列说法不正确的是( )| A. | 电阻R1两端的电压为50V | B. | 二极管的反向耐压值应大于50$\sqrt{2}$V | ||
| C. | 原线圈的输入功率为200W | D. | 通过R2的电流为$\sqrt{2}$A |
19.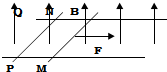 如图所示,两条足够长的光滑平行金属导轨水平放置导轨上,静止地放置两根质量相同、电阻相同的导体棒MN和PQ,两导体棒平行且垂直导轨,整个空间存在垂直于导轨平面的匀强磁场,不计导轨电阻,现在导体棒MN上施加一恒定的水平外力F,沿导轨向右运动,则下列说法正确的是( )
如图所示,两条足够长的光滑平行金属导轨水平放置导轨上,静止地放置两根质量相同、电阻相同的导体棒MN和PQ,两导体棒平行且垂直导轨,整个空间存在垂直于导轨平面的匀强磁场,不计导轨电阻,现在导体棒MN上施加一恒定的水平外力F,沿导轨向右运动,则下列说法正确的是( )
 如图所示,两条足够长的光滑平行金属导轨水平放置导轨上,静止地放置两根质量相同、电阻相同的导体棒MN和PQ,两导体棒平行且垂直导轨,整个空间存在垂直于导轨平面的匀强磁场,不计导轨电阻,现在导体棒MN上施加一恒定的水平外力F,沿导轨向右运动,则下列说法正确的是( )
如图所示,两条足够长的光滑平行金属导轨水平放置导轨上,静止地放置两根质量相同、电阻相同的导体棒MN和PQ,两导体棒平行且垂直导轨,整个空间存在垂直于导轨平面的匀强磁场,不计导轨电阻,现在导体棒MN上施加一恒定的水平外力F,沿导轨向右运动,则下列说法正确的是( )| A. | 最终两导体棒都做匀速直线运动 | |
| B. | 最终两导体棒都做匀加速直线运动 | |
| C. | 导体棒MN上的电流一直增大 | |
| D. | 导体棒PQ上的电流先不断增大后保持不变 |
17.下列说法中正确的是( )
| A. | 扩散现象只发生在液体和气体中 | |
| B. | 从微观角度看气体的压强大小由分子的平均动能决定 | |
| C. | 在一定温度下,某种液体的饱和汽压是一定的 | |
| D. | 某种气体在温度升高的过程中对外放出热量是可能的 |
 如图,MNPQ是一块截面为正方形的玻璃砖,其边长MN=60cm,一束激光沿AB射到玻璃砖的MQ面上(入射点为B),进入玻璃砖后在QP面上的F点(图中未画出)发生全反射,恰沿DC方向射出.其中B为MQ的中点,∠ABM=30°,PD=15cm,∠CDN=30°求
如图,MNPQ是一块截面为正方形的玻璃砖,其边长MN=60cm,一束激光沿AB射到玻璃砖的MQ面上(入射点为B),进入玻璃砖后在QP面上的F点(图中未画出)发生全反射,恰沿DC方向射出.其中B为MQ的中点,∠ABM=30°,PD=15cm,∠CDN=30°求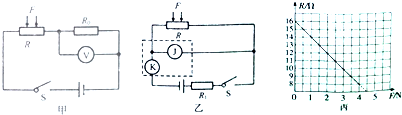

 如图所示,汽车在进行撞击实验时,安全气囊内迅速产生大量氮气而打开,气囊表面的气孔开始排气,若气囊表面有n个面积均为S的气孔,密度为ρ的氮气以速度v从气孔排出,氮气的摩尔质量为M,阿伏加德罗常数为NA,则在短时间t内排除的氮气分子数为$\frac{nSvtρ{N}_{A}}{M}$,设气囊内氮气不与外界进行热交换,则排气过程中气囊内温度降低(选填“升高”“不变”或“降低”)
如图所示,汽车在进行撞击实验时,安全气囊内迅速产生大量氮气而打开,气囊表面的气孔开始排气,若气囊表面有n个面积均为S的气孔,密度为ρ的氮气以速度v从气孔排出,氮气的摩尔质量为M,阿伏加德罗常数为NA,则在短时间t内排除的氮气分子数为$\frac{nSvtρ{N}_{A}}{M}$,设气囊内氮气不与外界进行热交换,则排气过程中气囊内温度降低(选填“升高”“不变”或“降低”)