题目内容
15．
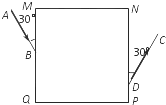如图，MNPQ是一块截面为正方形的玻璃砖，其边长MN=60cm，一束激光沿AB射到玻璃砖的MQ面上（入射点为B），进入玻璃砖后在QP面上的F点（图中未画出）发生全反射，恰沿DC方向射出．其中B为MQ的中点，∠ABM=30°，PD=15cm，∠CDN=30°求（1）QP面上的反射点F到Q点的距离QF；
（2）激光束在玻璃砖内的传播速度（真空中光速c=3.0×108m/s，结果可用根式表示）
分析 （1）激光束在玻璃砖内发生两次折射、一次全反射，画出光路图示意图如图．根据几何知识求得QF；
（2）由几何关系求出折射角的正弦，由折射定律n=$\frac{sini}{sinr}$求出折射率．由n=$\frac{c}{v}$求激光束在玻璃砖内的传播速度．
解答 解：（1）光路示意图如图所示，反射点为F．
由几何关系得 tanr=$\frac{QB}{QF}$=$\frac{PD}{PF}$…①．
且QF+FP=QP=MN…②
代入数据得 QF=40cm…③
（2）由几何关系可得 tanr=$\frac{3}{4}$，得 sinr=0.6…④
由折射定律得
n=$\frac{sini}{sinr}$=$\frac{sin60°}{0.6}$$\frac{5\sqrt{3}}{6}$…⑤
由n=$\frac{c}{v}$…⑥
得激光束在玻璃砖内的传播速度 v=$\frac{6\sqrt{3}}{5}×1{0}^{8}$m/s…⑦
答：
（1）QP面上的反射点F到Q点的距离QF是40cm；
（2）激光束在玻璃砖内的传播速度是$\frac{6\sqrt{3}}{5}×1{0}^{8}$m/s．
点评 对于几何光学问题，关键是正确画出光路图，灵活运用几何知识辅助求解，同时要掌握关于折射率的两个公式，并能熟练运用．
练习册系列答案
相关题目
6．根据热力学定律，下列说法正确的是（ ）
| A． | 电冰箱的工作表明，热量可以从低温物体向高温物体传递 | |
| B． | 空调机在制冷过程中，从室内吸收的热量少于向室外放出的热量 | |
| C． | 科技的不断进步使得人类有可能生产出单一热源的热机 | |
| D． | 即使没有漏气、摩擦、不必要的散热等损失，热机也不可以把燃料产生的内能全部转化为机械能 | |
| E． | 对能源的过度消耗使自然界的能量不断减少，形成“能源危机” |
3．
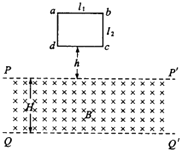如图所示，矩形平面导线框abcd位于竖直平面内，水平边ab长l1，竖直边bc长l2，线框质量为m，电阻为R．线框下方有一磁感应强度为B、方向与线框平面垂直的匀强磁场区域，该区域的上、下边界PP′和QQ′均与ab平行，两边界间的距离为H，H＞l2．让线框从dc边距边界PP′的距离为h处自由下落，已知在dc边进人磁场后、ab边到达边界PP′前的某一时刻，线框的速度已达到这一阶段的最大值，重力加速度为g，则（ ）
如图所示，矩形平面导线框abcd位于竖直平面内，水平边ab长l1，竖直边bc长l2，线框质量为m，电阻为R．线框下方有一磁感应强度为B、方向与线框平面垂直的匀强磁场区域，该区域的上、下边界PP′和QQ′均与ab平行，两边界间的距离为H，H＞l2．让线框从dc边距边界PP′的距离为h处自由下落，已知在dc边进人磁场后、ab边到达边界PP′前的某一时刻，线框的速度已达到这一阶段的最大值，重力加速度为g，则（ ）| A． | 当dc边刚进磁场时，线框速度为$\sqrt{2gh}$ | |
| B． | 当ab边刚到达边界PP′时，线框速度为$\frac{mgR}{{B}^{2}{{l}_{2}}^{2}}$ | |
| C． | 当dc边刚到达边界QQ′时，线框速度为$\sqrt{（\frac{mgR}{{B}^{2}{{l}_{1}}^{2}}）^{2}+2g（H-{l}_{2}）}$ | |
| D． | 从线框开始下落到dc边刚到达边界的QQ′过程中，线框产生的焦耳热为mg（h+l2）-$\frac{{m}^{3}{g}^{2}{R}^{2}}{2{B}^{4}{{l}_{2}}^{4}}$ |
10．
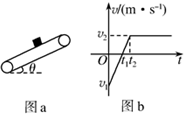已知一足够长的传送带倾角为θ，以一定的速度匀速运动，某时刻在传送带适当的位置放上具有一定初速度、质量为m的物块（如图a所示）以此时为t=0时刻，记录小物块之后在传送带上运动的速度随时间的变化关系，如图b所示（图中取沿斜面向上的运动方向为正方向，其中两坐标大小|v1|＞v2），已知传送带的速度保持不变，下列判断正确的是（ ）
已知一足够长的传送带倾角为θ，以一定的速度匀速运动，某时刻在传送带适当的位置放上具有一定初速度、质量为m的物块（如图a所示）以此时为t=0时刻，记录小物块之后在传送带上运动的速度随时间的变化关系，如图b所示（图中取沿斜面向上的运动方向为正方向，其中两坐标大小|v1|＞v2），已知传送带的速度保持不变，下列判断正确的是（ ）| A． | 0～t1时间内，物块对传送带做正功 | |
| B． | 物块与传送带间的动摩擦因数μ小于tanθ | |
| C． | 0～t2时间内，合力对物块做功为$\frac{1}{2}$mv22-$\frac{1}{2}$mv12 | |
| D． | 0～t1时间内，系统产生的热量一定比物块动能的减少量大 |
20．如图甲所示，有一绝缘的竖直圆环，圆环上均匀分布着正电荷．一光滑细杆沿垂直圆环平面的轴线穿过圆环，细杆上套有一个质量为m=10g的带正电的小球，小球所带电荷量q=5.0×10-4C，让小球从C点由静止释放，其沿细杆由C经B向A运动的v-t图象如图乙所示．且已知小球运动到B点时，速度图象的切线斜率最大（图中标出了该切线）．下列说法正确的是（ ）
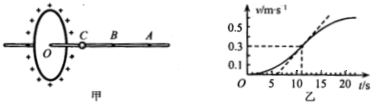
| A． | 在O点右侧杆上，B点场强最大，场强大小为E=1.2V/m | |
| B． | 由C到A的过程中，小球的电势能先减小后变大 | |
| C． | 沿着C到A的方向，电势先降低后升高 | |
| D． | C、B两点间的电势差UCB=0.9V |
7．
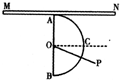如图，ABC为某半圆形透明介质与空气的分界面，其圆心为O，直径为d．MN为紧靠A点并与直径AB垂直放置的足够长光屏，调节激光器，使PO光线从透明介质右侧弧面沿某一半径方向射向圆心O，当光线PO在O点的入射角为θ时，发现光屏MN的左右两侧均出现亮点，且左、右两侧亮点到A点的距离分别为$\frac{d}{2}$、$\frac{\sqrt{3}d}{2}$，则由以上信息可知（ ）
如图，ABC为某半圆形透明介质与空气的分界面，其圆心为O，直径为d．MN为紧靠A点并与直径AB垂直放置的足够长光屏，调节激光器，使PO光线从透明介质右侧弧面沿某一半径方向射向圆心O，当光线PO在O点的入射角为θ时，发现光屏MN的左右两侧均出现亮点，且左、右两侧亮点到A点的距离分别为$\frac{d}{2}$、$\frac{\sqrt{3}d}{2}$，则由以上信息可知（ ）| A． | θ=60° | |
| B． | 该透明介质的折射率n=$\sqrt{3}$ | |
| C． | 若增大θ，光屏MN上左侧亮点可能消失 | |
| D． | 若θ=45°，光屏MN上左、右两侧亮点到A点的距离相等 |
4．嫦娥三号携带“玉兔”探测车在月球虹湾成功软着陆．在实施软着陆过程中，嫦娥三号离月球表面4m高时最后一次悬停，确认着陆点．若总质量为M的嫦娥三号在最后一次悬停时，反推力发动机对其提供的反推力为F，已知引力常量为G，月球半径为R，则月球的密度为（ ）
| A． | $\frac{3F}{4πGMR}$ | B． | $\frac{3F}{4πGM{R}^{2}}$ | C． | $\frac{3F}{4πGM{R}^{4}}$ | D． | $\frac{3GM}{4πF{R}^{5}}$ |
5．如图为小型交流发电机的示意图，线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动，转速为50r/s，线圈的电阻为r=20Ω，电阻R=100Ω，R0=10Ω，降压变压器原副线圈匝数比为10：1，电压表的示数为10V，如果从图示位置开始计时，下列说法中正确的是（ ）
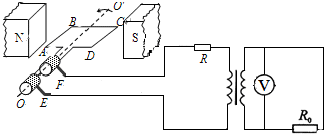
| A． | 变压器原线圈两端的电压为100 V | |
| B． | 电阻R的功率为10W | |
| C． | 电动势的有效值为110 V | |
| D． | 电动势瞬时值表达式为e=112$\sqrt{2}$cos100πtV |