题目内容

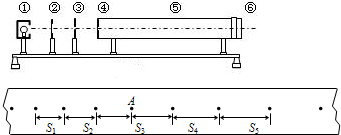
如图所示，某同学在做“研究匀变速直线运动”实验中，由打点计时器得到表示小车运动过程的一条清晰纸带，纸带上两相邻计数点间的时间间隔为T=0.10s，其中s1=7.05cm、s2=7.68cm、s3=8.31cm、s4=8.95cm、s5=9.58cm、s6=10.20cm，则打A点时小车瞬时速度的大小是
0.86
0.86
m/s，小车运动的加速度大小是
0.63
0.63
m/s2（计算结果保留两位有效数字）．
分析：根据某段时间内的平均速度等于中间时刻的瞬时速度求出A点的瞬时速度，通过连续相等时间内的位移之差是一恒量求出加速度的大小．
解答：解：A点的瞬时速度vA=
s3+s4
2T
=
(8.31+8.95)×10-2
0.2
m/s≈0.86m/s．
根据△x=aT2，运用逐差法得，a=
(s4+s5+s6)-(s1+s2+s3)
9T2
=
(8.95+9.58+10.20)×10-2-(7.05+7.68+8.31)×10-2
9×0.01
≈0.63m/s2．
故答案为：0.86，0.63
点评：解决本题的关键掌握纸带的处理方法，会通过纸带求解加速度和瞬时速度，计算时注意有效数字的保留．
练习册系列答案
相关题目
如图所示是某同学在做匀变速直线运动实验中获得的一条纸带．

（1）已知打点计时器电源频率为50Hz，则纸带上打相邻两点的时间间隔为
0.02s
0.02s
．
（2）A、B、C、D是纸带上四个计数点，每两个相邻计数点间有四个点没有画出，从图中读出A、B两点间距x=
0.65
0.65
cm；C点对应的速度是
0.10
0.10
 m/s，加速度是
0.30
0.30
 m/s2（速度和加速度的计算结果保留两位有效数字）
如图所示，某同学在做“研究匀变速直线运动”实验中，由打点计时器得到表示小车运动过程的一条清晰纸带，纸带上两相邻计数点的时间间隔为T=0.10s，其中S1=7.05cm、S2=7.68cm、S3=8.33cm、S4=8.95cm、S5=9.61cm、S6=10.26cm，则打A点时小车瞬时速度的大小是
0.86
0.86
m/s，小车运动的加速度计算表达式为
(s4+s5+s6)-(s1+s2+s3)
9T2
(s4+s5+s6)-(s1+s2+s3)
9T2
，加速度的大小是
0.64
0.64
m/s2（计算结果保留两位有效数字）．
如图所示是某同学在做“研究平抛物体的运动”的实验时得到的物体运动轨迹的一部分，O、a、b、c是运动轨迹上的四点，以O点为坐标原点建立直角坐标系（轨迹和坐标轴上的虚线表示有所省略），a、b、c三点的坐标如图，则小球平抛的初速度v0=
2.0
2.0
m/s，小球开始做平抛运动时的位置
是
是
（选填“是”或“不是”） O点． （g=10m/s2）
如图所示，某同学在做“研究匀变速直线运动”的实验中，由打点计时器得到表示小车运动过程的一条清晰纸带，纸带上两相邻计数点的时间间隔为T=0.10s，其中x1=7.10cm、x2=7.70cm、x3=8.30cm、x4=8.90cm、x5=9.50cm、x6=10.10cm，则：

（1）计算vA的公式为vA=
略
略
，vA大小为
0.920
0.920
m/s；（取三位有效数字）
（2）小车的加速度的大小是a=
0.60
0.60
m/s2；（取两位有效数字）
（3）如果当时电网中交变电流的频率是f=51Hz，而做实验的同学并不知道，那么加速度的测量值与实际值相比
偏小
偏小
（选填：偏大、偏小或不变）．
（1）如图所示，在“用双缝干涉测光的波长”实验中，光具座上放置的光学元件依次为①光源、②
 
、③
 
、④
 
、⑤遮光筒、⑥光屏．对于某种单色光，为增加相邻亮纹（暗纹）间的距离，可采取
 
或
 
的方法．
（2）如图所示，某同学在做“研究匀变速直线运动”实验中，由打点计时器得到表示小车运动过程的一条清晰纸带，纸带上两相邻计数点的时间间隔为T=0.10s，其中S1=7.05cm、S2=7.68cm、S3=8.33cm、S4=8.95cm、S5=9.61cm、S6=10.26cm，则A点处瞬时速度的大小是
 
m/s，小车运动的加速度计算表达式为
 
，加速度的大小是
 
m/s2（计算结果保留两位有效数字）．
精英家教网

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网