题目内容
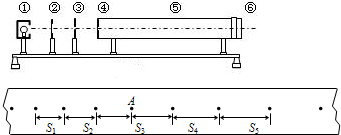
如图所示，某同学在做“研究匀变速直线运动”实验中，由打点计时器得到表示小车运动过程的一条清晰纸带，纸带上两相邻计数点的时间间隔为T=0.10s，其中S1=7.05cm、S2=7.68cm、S3=8.33cm、S4=8.95cm、S5=9.61cm、S6=10.26cm，则打A点时小车瞬时速度的大小是
，加速度的大小是
0.86
0.86
m/s，小车运动的加速度计算表达式为| (s4+s5+s6)-(s1+s2+s3) |
| 9T2 |
| (s4+s5+s6)-(s1+s2+s3) |
| 9T2 |
0.64
0.64
m/s2（计算结果保留两位有效数字）．分析：纸带实验中，若纸带匀变速直线运动，测得纸带上的点间距，利用匀变速直线运动的推论，可计算出打出某点时纸带运动的瞬时速度和加速度．
解答：解：利用匀变速直线运动的推论得：
vA=
=0.86m/s．
由于相邻的计数点间的位移之差不等，故采用逐差法求解加速度．
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小，
得：s4-s1=3a1T2
s5-s2=3a2T2
s6-s3=3a3T2
为了更加准确的求解加速度，我们对三个加速度取平均值
得：a=
（a1+a2+a3）
小车运动的加速度计算表达式为a=
代入数据得a=0.64m/s2．
故答案为：0.86，
，0.64．
vA=
| s3+s4 |
| 2t |
由于相邻的计数点间的位移之差不等，故采用逐差法求解加速度．
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小，
得：s4-s1=3a1T2
s5-s2=3a2T2
s6-s3=3a3T2
为了更加准确的求解加速度，我们对三个加速度取平均值
得：a=
| 1 |
| 3 |
小车运动的加速度计算表达式为a=
| (s4+s5+s6)-(s1+s2+s3) |
| 9T2 |
代入数据得a=0.64m/s2．
故答案为：0.86，
| (s4+s5+s6)-(s1+s2+s3) |
| 9T2 |
点评：要注意单位的换算和有效数字的保留．
能够运用逐差法求解加速度．
能够运用逐差法求解加速度．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
相关题目
如图所示是某同学在做“研究平抛物体的运动”的实验时得到的物体运动轨迹的一部分，O、a、b、c是运动轨迹上的四点，以O点为坐标原点建立直角坐标系（轨迹和坐标轴上的虚线表示有所省略），a、b、c三点的坐标如图，则小球平抛的初速度v0=
