题目内容
5.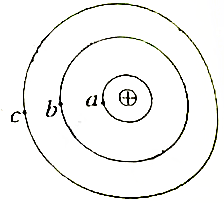 如图所示,a、b、c是氢原子的核外电子绕核运动的三个可能轨道,取无穷远电子的电势能为零,电子在a、b、c三个轨道时对应的电势能分别为-13.6eV、-3.4eV、-1.51eV,由于某种因素(如加热或光照)的影响,电子会沿椭圆轨道跃迁到离核更远的轨道上运动,求:
如图所示,a、b、c是氢原子的核外电子绕核运动的三个可能轨道,取无穷远电子的电势能为零,电子在a、b、c三个轨道时对应的电势能分别为-13.6eV、-3.4eV、-1.51eV,由于某种因素(如加热或光照)的影响,电子会沿椭圆轨道跃迁到离核更远的轨道上运动,求:(1)a、b、c三点的电势大小;
(2)a、b间,b、c间电势差的大小.
分析 (1)已知电势能,根据公式φ=$\frac{{E}_{p}}{q}$求解电势.
(2)根据电势差等于电势之差,求解即可.
解答 解:(1)a、b、c三点的电势大小分别为
φa=$\frac{Epa}{-e}$=$\frac{-13.6eV}{-e}$=13.6V
φb=$\frac{{E}_{pb}}{-e}$=$\frac{-3.4eV}{-e}$=3.4V
φc=$\frac{{E}_{pc}}{-e}$=$\frac{-1.51eV}{-e}$=1.51V
(2)a、b间电势差的大小 Uab=φa-φb=10.2V
b、c间电势差的大小 Ubc=φb-φc=1.89V
答:
(1)a、b、c三点的电势大小分别为13.6V,3.4V和1.51V;
(2)a、b间,b、c间电势差的大小分别为10.2V和1.89V.
点评 解决本题的关键要掌握电势的定义式φ=$\frac{{E}_{p}}{q}$,并能熟练运用,运用此公式时要注意各个量都要符号运算.

练习册系列答案
相关题目
15.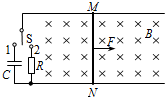 如图所示,宽为L的水平光滑金属轨道上放置一根质量为m的导体棒MN,轨道左端通过一个单刀双掷开关与一个电容器和一个阻值为R的电阻连接,匀强磁场的方向与轨道平面垂直,磁感应强度大小为B,电容器的电容为C,金属轨道和导体棒的电阻不计.现将开关拨向“1”,导体棒MN在水平向右的恒力F作用下由静止开始运动,经时间t0后,将开关S拨向“2”,再经时间t,导体棒MN恰好开始匀速向右运动.下列说法正确的是( )
如图所示,宽为L的水平光滑金属轨道上放置一根质量为m的导体棒MN,轨道左端通过一个单刀双掷开关与一个电容器和一个阻值为R的电阻连接,匀强磁场的方向与轨道平面垂直,磁感应强度大小为B,电容器的电容为C,金属轨道和导体棒的电阻不计.现将开关拨向“1”,导体棒MN在水平向右的恒力F作用下由静止开始运动,经时间t0后,将开关S拨向“2”,再经时间t,导体棒MN恰好开始匀速向右运动.下列说法正确的是( )
 如图所示,宽为L的水平光滑金属轨道上放置一根质量为m的导体棒MN,轨道左端通过一个单刀双掷开关与一个电容器和一个阻值为R的电阻连接,匀强磁场的方向与轨道平面垂直,磁感应强度大小为B,电容器的电容为C,金属轨道和导体棒的电阻不计.现将开关拨向“1”,导体棒MN在水平向右的恒力F作用下由静止开始运动,经时间t0后,将开关S拨向“2”,再经时间t,导体棒MN恰好开始匀速向右运动.下列说法正确的是( )
如图所示,宽为L的水平光滑金属轨道上放置一根质量为m的导体棒MN,轨道左端通过一个单刀双掷开关与一个电容器和一个阻值为R的电阻连接,匀强磁场的方向与轨道平面垂直,磁感应强度大小为B,电容器的电容为C,金属轨道和导体棒的电阻不计.现将开关拨向“1”,导体棒MN在水平向右的恒力F作用下由静止开始运动,经时间t0后,将开关S拨向“2”,再经时间t,导体棒MN恰好开始匀速向右运动.下列说法正确的是( )| A. | 开关拨向“1”时,金属棒做加速度逐渐减小的加速运动 | |
| B. | t0时刻电容器所带的电荷量为$\frac{CBLF{t}_{0}}{m+{B}^{2}{L}^{2}C}$ | |
| C. | 开关拨向“2”后,导体棒匀速运动的速率为$\frac{FR}{{B}^{2}{L}^{2}}$ | |
| D. | 开关拨向“2”后t时间内,导体棒通过的位移为$\frac{FR}{{B}^{2}{L}^{2}}$(t+$\frac{m{t}_{0}}{m+{B}^{2}{L}^{2}C}$-$\frac{mR}{{B}^{2}{L}^{2}}$) |
16.如图为一定质量的某种气体的p-t图象.在A、B、C三个状态中,下列判断正确的是( )
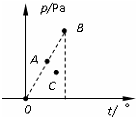

| A. | 体积最大的是C状态 | |
| B. | 体积最大的是B状态 | |
| C. | A、B两状态体积一样 | |
| D. | A 状态变到B状态,外界对气体做功值等于气体内能增加 |
13.许多物理学家的科学发现推动了人类历史的进步,下列关于几位物理学家所作出的科学贡献的叙述,正确的是( )
| A. | 法拉第通过实验独立发现了利用磁场产生电流的条件和规律 | |
| B. | 安培在研究磁场与电流的相互作用方面作出了杰出的贡献 | |
| C. | 奥斯特发现了点电荷之间的相互作用规律 | |
| D. | 库伦提出了磁场对运动电荷的作用力公式 |
20.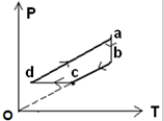 一定质量的理想气体的状态经历了如图所示的abcda循环过程,其中bc的延长线通过原点,cd垂直于ab且与水平轴平行,da与bc平行,则以下说法中正确的是( )
一定质量的理想气体的状态经历了如图所示的abcda循环过程,其中bc的延长线通过原点,cd垂直于ab且与水平轴平行,da与bc平行,则以下说法中正确的是( )
 一定质量的理想气体的状态经历了如图所示的abcda循环过程,其中bc的延长线通过原点,cd垂直于ab且与水平轴平行,da与bc平行,则以下说法中正确的是( )
一定质量的理想气体的状态经历了如图所示的abcda循环过程,其中bc的延长线通过原点,cd垂直于ab且与水平轴平行,da与bc平行,则以下说法中正确的是( )| A. | a→b过程中,气体既不吸热也不放热 | |
| B. | 气体从b→c单位体积内分子数没有变化 | |
| C. | c→d过程中,气态分子的平均动能减小 | |
| D. | d→a过程中,气体体积保持不变 |
10.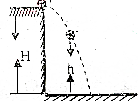 如图,质量为m的足球以速度为V0离开桌面,桌面离地面高度为H,当它经过离地面高度为h时,若以桌面为参考面且不计空气阻力,则足球( )
如图,质量为m的足球以速度为V0离开桌面,桌面离地面高度为H,当它经过离地面高度为h时,若以桌面为参考面且不计空气阻力,则足球( )
 如图,质量为m的足球以速度为V0离开桌面,桌面离地面高度为H,当它经过离地面高度为h时,若以桌面为参考面且不计空气阻力,则足球( )
如图,质量为m的足球以速度为V0离开桌面,桌面离地面高度为H,当它经过离地面高度为h时,若以桌面为参考面且不计空气阻力,则足球( )| A. | 机械能$\frac{1}{2}$mV02 | B. | 机械能为$\frac{1}{2}$mV02+mgH | ||
| C. | 动能为$\frac{1}{2}$mV02+mg(H-h) | D. | 动能为mg(H-h) |
2.已知地球的半径为r,自转周期为T;某一颗地球同步卫星绕地球运动的轨道半径为R;万有引力常量为G;如果把该卫星的运动看作匀速圆周运动,则( )
| A. | 地球的质量为$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$ | B. | 地球的质量为$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$ | ||
| C. | 地球的平均密度为$\frac{3π}{G{T}^{2}}$ | D. | 地球的平均密度为$\frac{3π{R}^{3}}{G{T}^{2}{r}^{3}}$ |
19.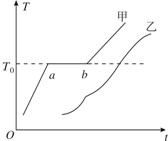 固体甲和固体乙在一定压强下的熔解曲线如图所示,横轴表示时间t,纵轴表示温度T.下列判断正确的有 ( )
固体甲和固体乙在一定压强下的熔解曲线如图所示,横轴表示时间t,纵轴表示温度T.下列判断正确的有 ( )
 固体甲和固体乙在一定压强下的熔解曲线如图所示,横轴表示时间t,纵轴表示温度T.下列判断正确的有 ( )
固体甲和固体乙在一定压强下的熔解曲线如图所示,横轴表示时间t,纵轴表示温度T.下列判断正确的有 ( )| A. | 固体甲一定是晶体,固体乙一定是非晶体 | |
| B. | 固体甲不一定有确定的几何外形,固体乙一定没有确定的几何外形 | |
| C. | 在热传导方面固体甲一定表现出各向异性,固体乙一定表现出各向同性 | |
| D. | 固体甲和固体乙的化学成分有可能相同 | |
| E. | 图线甲中ab段温度不变,所以甲的内能不变 |
