题目内容
2.已知地球的半径为r,自转周期为T;某一颗地球同步卫星绕地球运动的轨道半径为R;万有引力常量为G;如果把该卫星的运动看作匀速圆周运动,则( )| A. | 地球的质量为$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$ | B. | 地球的质量为$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$ | ||
| C. | 地球的平均密度为$\frac{3π}{G{T}^{2}}$ | D. | 地球的平均密度为$\frac{3π{R}^{3}}{G{T}^{2}{r}^{3}}$ |
分析 研究同步卫星绕地球圆周运动,利用万有引力提供向心力可求出地球的质量.根据密度定义式求解地球的平均密度;
解答 解:A、研究同步卫星绕地球圆周运动,利用万有引力提供向心力得:
$\frac{GMm}{{R}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$R
M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$,故A错误,B正确
C、根据密度定义式ρ=$\frac{M}{V}$=$\frac{3π{R}^{3}}{G{T}^{2}{r}^{3}}$,故C错误,D正确;
故选:BD.
点评 解决本题的关键掌握万有引力提供向心力,注意不同的圆周运动对应不同的轨道半径,注意星球半径和轨道半径的区别.

练习册系列答案
相关题目
7.如图甲所示,在x轴上有一个点电荷Q(图中未画出),O、A、B为轴上三点,放在A、B两点的试探电荷受到的电场力跟试探电荷所带电荷量的关系如图乙所示,则( )
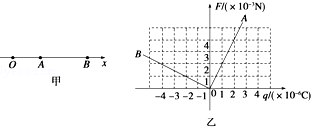

| A. | A点的电场强度大小为2×103N/C | B. | B点的电场强度大小为2×103N/C | ||
| C. | 点电荷Q在A、B之间 | D. | 点电荷Q在A、O之间 |
8.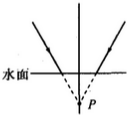 如图所示,一束圆锥体形的单色光在空气中传播,将会聚于P,在到达P之前若先进入水中,圆锤的轴垂直于水面,圆锥顶角为θ,P到水面的距离一定,则( )(θ很小时,θ=sinθ=tanθ)
如图所示,一束圆锥体形的单色光在空气中传播,将会聚于P,在到达P之前若先进入水中,圆锤的轴垂直于水面,圆锥顶角为θ,P到水面的距离一定,则( )(θ很小时,θ=sinθ=tanθ)
 如图所示,一束圆锥体形的单色光在空气中传播,将会聚于P,在到达P之前若先进入水中,圆锤的轴垂直于水面,圆锥顶角为θ,P到水面的距离一定,则( )(θ很小时,θ=sinθ=tanθ)
如图所示,一束圆锥体形的单色光在空气中传播,将会聚于P,在到达P之前若先进入水中,圆锤的轴垂直于水面,圆锥顶角为θ,P到水面的距离一定,则( )(θ很小时,θ=sinθ=tanθ)| A. | 若θ 很大,锥体内的光线不能全部聚于一点 | |
| B. | 若θ 很小,锥体内的光线不能全部聚于一点 | |
| C. | θ 很大时,光线与轴的交点从P点开始至无限远 | |
| D. | θ 很小时,光线与轴的交点无限靠近P |
14.关于经典力学的局限性,下列说法正确的是( )
| A. | 经典力学不能很好地描述微观粒子运动的规律 | |
| B. | 地球以3×104m/s的速度绕太阳公转时,经典力学就不适用了 | |
| C. | 在所有天体的引力场中,牛顿的引力理论都是适用的 | |
| D. | 20世纪初,爱因斯坦建立的相对论完全否定了经典力学的观念和结论 |
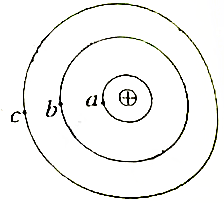 如图所示,a、b、c是氢原子的核外电子绕核运动的三个可能轨道,取无穷远电子的电势能为零,电子在a、b、c三个轨道时对应的电势能分别为-13.6eV、-3.4eV、-1.51eV,由于某种因素(如加热或光照)的影响,电子会沿椭圆轨道跃迁到离核更远的轨道上运动,求:
如图所示,a、b、c是氢原子的核外电子绕核运动的三个可能轨道,取无穷远电子的电势能为零,电子在a、b、c三个轨道时对应的电势能分别为-13.6eV、-3.4eV、-1.51eV,由于某种因素(如加热或光照)的影响,电子会沿椭圆轨道跃迁到离核更远的轨道上运动,求: 一个滴管,其尾部套有一个弹性橡胶球,先把滴管的玻璃嘴放入水中,然后积压释放橡胶球,使水进入滴管内部,图中滴管内部的液面高处器皿内的液面0.15m,那么橡胶球内气体的压强是多少(设大气压p0=1.0×105Pa)?如果把这套装置移到高山上,滴管吸水的效果有什么变化?为什么?
一个滴管,其尾部套有一个弹性橡胶球,先把滴管的玻璃嘴放入水中,然后积压释放橡胶球,使水进入滴管内部,图中滴管内部的液面高处器皿内的液面0.15m,那么橡胶球内气体的压强是多少(设大气压p0=1.0×105Pa)?如果把这套装置移到高山上,滴管吸水的效果有什么变化?为什么?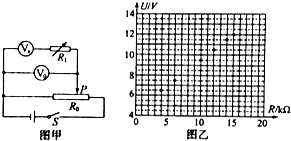 一个电压表V,量程约为5V,有清晰刻度但没有示数,内电阻约为10kΩ,某同学想准确地测出其量程和内阻,可以使用的实验器材如下:
一个电压表V,量程约为5V,有清晰刻度但没有示数,内电阻约为10kΩ,某同学想准确地测出其量程和内阻,可以使用的实验器材如下: