题目内容
20.为了“探究动能改变与合外力做功”的关系,某同学设计了如下实验方案:第一步:把带有定滑轮的木板有滑轮的一端垫起,把质量为M的滑块通过细绳与质量为m的带夹重锤跨过定滑轮相连,重锤夹后连一穿过打点计时器的纸带,调整木板倾角,直到轻推滑块后,滑块沿木板向下匀速运动,如图甲所示.
第二步:保持长木板的倾角不变,将打点计时器安装在长木板靠近滑轮处,取下细绳和重锤,将滑块与纸带相连,使纸带穿过打点计时器,然后接通电源,释放滑块,使之从静止开始向下加速运动,打出纸带,如图乙所示.打出的纸带如图丙所示.

请回答下列问题:
(1)已知O、A、B、C、D、E、F相邻计数点间的时间间隔为△t,根据纸带求滑块速度,打点计时器打B点时滑块速度vB=$\frac{{x}_{3}-{x}_{1}}{2△t}$.
(2)已知重锤质量为m,当地的重力加速度为g,要测出某一过程合外力对滑块做的功还必须测出这一过程滑块运动的位移x(写出物理名称及符号,只写一个物理量),合外力对滑块做功的表达式W合=mgx.
(3)算出滑块运动OA、OB、OC、OD、OE段合外力对滑块所做的功W以及在A、B、C、D、E各点的速度v,以v2为纵轴、W为横轴建立直角坐标系,描点作出v2-W图象,可知该图象是一条过原点的倾斜的直线,根据图象还可求得滑块的质量.
分析 (1)用平均速度代替瞬时速度去求解AB点的速度;
(2)合外力为重物的重力,要求出外力对滑块做的功还必须测出这一过程滑块的位移x,根据W=Fx即可求解;
(3)根据做功公式求出W与v2的关系式即可求解.
解答 解:(1)匀变速直线运动中时间中点的速度等于该过程中的平均速度,故:
vB=$\frac{{x}_{3}-{x}_{1}}{2△t}$
(2)本题运动过程中,物块受到的合力为重力,要求合力做的功,则还需要测出这一过程滑块运动的位移x,则合外力对滑块做功的表达式W合=mgx,
(3)合外力做的功为W=mgx=$\frac{1}{2}m{v}^{2}$,
所以v2=$\frac{2}{m}$W,则v2-W图象是一条过原点的倾斜的直线,
根据图象课求得直线斜率为k,所以m=$\frac{2}{k}$,即根据图象可以求得滑块的质量.
故答案为:(1)$\frac{{x}_{3}-{x}_{1}}{2△t}$;(2)运动的位移x;mgx;(3)过原点的倾斜的直线;滑块的质量
点评 本题主要考查了打点计时器中求瞬时速度的方法,能根据做功公式求出W与v2的关系式,根据图象的斜率求解质量,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.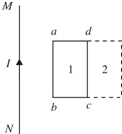 如图所示,通有恒定电流的导线MN与闭合线框共面,第一次将线框由位置1平移到位置2,第二次将线框绕cd边翻转到位置2,设先后两次通过线框的磁通量变化分别为△Φ1和△Φ2,则( )
如图所示,通有恒定电流的导线MN与闭合线框共面,第一次将线框由位置1平移到位置2,第二次将线框绕cd边翻转到位置2,设先后两次通过线框的磁通量变化分别为△Φ1和△Φ2,则( )
 如图所示,通有恒定电流的导线MN与闭合线框共面,第一次将线框由位置1平移到位置2,第二次将线框绕cd边翻转到位置2,设先后两次通过线框的磁通量变化分别为△Φ1和△Φ2,则( )
如图所示,通有恒定电流的导线MN与闭合线框共面,第一次将线框由位置1平移到位置2,第二次将线框绕cd边翻转到位置2,设先后两次通过线框的磁通量变化分别为△Φ1和△Φ2,则( )| A. | △Φ1>△Φ2 | B. | △Φ1=△Φ2 | C. | △Φ1<△Φ2 | D. | 无法确定 |
5.某人用手将质量为1kg的物体由静止向上提起1m,这时物体的速度为2m/s,取g=10m/s2,则下列说法中正确的是( )
| A. | 物体的动能增加了2J | B. | 物体的重力势能增加了10J | ||
| C. | 物体的动能增加了10J | D. | 手对物体做的功为2J |
10.一艘在太空飞行的宇宙飞船,开动推进器后受到的推力是800N,开动5s的时间,速度的改变为2m/s,则宇宙飞船的质量为( )
| A. | 1000kg | B. | 2000kg | C. | 3000kg | D. | 4000kg |
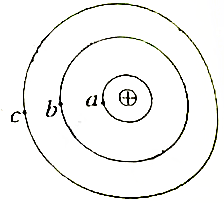 如图所示,a、b、c是氢原子的核外电子绕核运动的三个可能轨道,取无穷远电子的电势能为零,电子在a、b、c三个轨道时对应的电势能分别为-13.6eV、-3.4eV、-1.51eV,由于某种因素(如加热或光照)的影响,电子会沿椭圆轨道跃迁到离核更远的轨道上运动,求:
如图所示,a、b、c是氢原子的核外电子绕核运动的三个可能轨道,取无穷远电子的电势能为零,电子在a、b、c三个轨道时对应的电势能分别为-13.6eV、-3.4eV、-1.51eV,由于某种因素(如加热或光照)的影响,电子会沿椭圆轨道跃迁到离核更远的轨道上运动,求: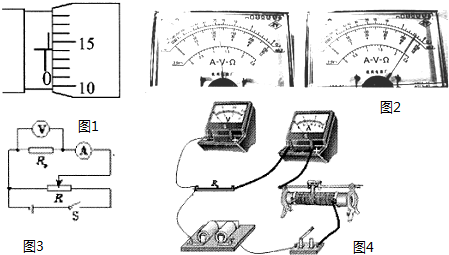
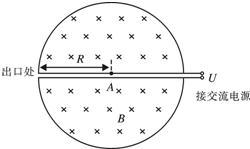 1932年,劳伦斯和利文斯设计出了回旋加速器.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计,磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生的粒子,质量为m、电荷量为+q,在加速电压为U的加速器中被加速,加速过程中不考虑相对论效应和重力作用,不计粒子的初速度.
1932年,劳伦斯和利文斯设计出了回旋加速器.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计,磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生的粒子,质量为m、电荷量为+q,在加速电压为U的加速器中被加速,加速过程中不考虑相对论效应和重力作用,不计粒子的初速度.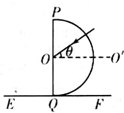 一同学用图示装置研究色散现象,半径为R的半圆形玻璃砖下端紧靠在足够大的EF上.O点为圆心,OO′为直径PQ的垂线.一束复色光沿半径方向与OO′成θ=30°角射向O点.已知复色光包含有折射率从n1=$\sqrt{2}$到n2=1.6的光束,光屏上出现了彩色光带.sin37°=0.6.
一同学用图示装置研究色散现象,半径为R的半圆形玻璃砖下端紧靠在足够大的EF上.O点为圆心,OO′为直径PQ的垂线.一束复色光沿半径方向与OO′成θ=30°角射向O点.已知复色光包含有折射率从n1=$\sqrt{2}$到n2=1.6的光束,光屏上出现了彩色光带.sin37°=0.6.