题目内容
15.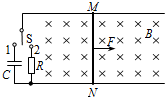 如图所示,宽为L的水平光滑金属轨道上放置一根质量为m的导体棒MN,轨道左端通过一个单刀双掷开关与一个电容器和一个阻值为R的电阻连接,匀强磁场的方向与轨道平面垂直,磁感应强度大小为B,电容器的电容为C,金属轨道和导体棒的电阻不计.现将开关拨向“1”,导体棒MN在水平向右的恒力F作用下由静止开始运动,经时间t0后,将开关S拨向“2”,再经时间t,导体棒MN恰好开始匀速向右运动.下列说法正确的是( )
如图所示,宽为L的水平光滑金属轨道上放置一根质量为m的导体棒MN,轨道左端通过一个单刀双掷开关与一个电容器和一个阻值为R的电阻连接,匀强磁场的方向与轨道平面垂直,磁感应强度大小为B,电容器的电容为C,金属轨道和导体棒的电阻不计.现将开关拨向“1”,导体棒MN在水平向右的恒力F作用下由静止开始运动,经时间t0后,将开关S拨向“2”,再经时间t,导体棒MN恰好开始匀速向右运动.下列说法正确的是( )| A. | 开关拨向“1”时,金属棒做加速度逐渐减小的加速运动 | |
| B. | t0时刻电容器所带的电荷量为$\frac{CBLF{t}_{0}}{m+{B}^{2}{L}^{2}C}$ | |
| C. | 开关拨向“2”后,导体棒匀速运动的速率为$\frac{FR}{{B}^{2}{L}^{2}}$ | |
| D. | 开关拨向“2”后t时间内,导体棒通过的位移为$\frac{FR}{{B}^{2}{L}^{2}}$(t+$\frac{m{t}_{0}}{m+{B}^{2}{L}^{2}C}$-$\frac{mR}{{B}^{2}{L}^{2}}$) |
分析 开关拨向“1”时,根据牛顿第二定律和电流的定义式,得到金属棒的加速度表达式,再分析其运动情况.由法拉第电磁感应定律求解MN棒产生的感应电动势,得到电容器的电压,从而求出电容器的电量.开关拨向“2”时,由平衡条件和安培力与速度的关系式,求解匀速运动的速率.由牛顿第二定律得到加速度的瞬时表达式,运用微元法求解位移.
解答 解:A、开关拨向“1”时,在极短时间△t内流过金属棒的电荷量为△Q,则电路中的瞬时电流为 I=$\frac{△Q}{△t}$
电容器的电压 U=BLv,电荷量 Q=CU,则△Q=C△U=CBL△v
可得 I=CBL$\frac{△v}{△t}$=CBLa
对金属棒,由牛顿第二定律得 F-BIL=ma
联立得金属棒的瞬时加速度为 a=$\frac{F}{m+C{B}^{2}{L}^{2}}$
则知金属棒的加速度不变,做匀加速直线运动,故A错误.
B、t0时刻电容器所带的电压 U=BLat0,电荷量 Q=CU,则得 Q=$\frac{CBLF{t}_{0}}{m+{B}^{2}{L}^{2}C}$,故B正确.
C、开关拨向“2”后,导体棒匀速运动时,有 F=$\frac{{B}^{2}{L}^{2}v}{R}$,则得v=$\frac{FR}{{B}^{2}{L}^{2}}$,故C正确.
D、开关拨向“2”后t时间内,根据牛顿第二定律得:F-$\frac{{B}^{2}{L}^{2}v}{R}$=ma=m$\frac{△v}{△t}$
则得 F△t-$\frac{{B}^{2}{L}^{2}v△t}{R}$=m△v
两边求和得:$\sum_{\;}^{\;}$(F△t-$\frac{{B}^{2}{L}^{2}v△t}{R}$)=$\sum_{\;}^{\;}$m△v
而$\sum_{\;}^{\;}$v△t=x,$\sum_{\;}^{\;}$△v=v
联立解得位移 x=$\frac{FR}{{B}^{2}{L}^{2}}$(t+$\frac{m{t}_{0}}{m+{B}^{2}{L}^{2}C}$-$\frac{mR}{{B}^{2}{L}^{2}}$).故D正确.
故选:BCD.
点评 解决本题的关键有两个:一是抓住电流的定义式,结合牛顿第二定律分析金属棒的加速度.二是运用微元法,求解金属棒的位移,其切入口是加速度的定义式.

 名校课堂系列答案
名校课堂系列答案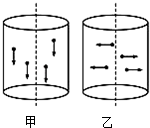 有同学想通过静电除尘的方法净化空气.她用玻璃圆桶密闭含灰尘的空气,圆桶的高和直径相等.方法一是:在圆桶顶面和底面间加上电压U,沿圆桶的轴线方向形成一个匀强电场,尘粒的运动方向如图甲所示;方法二是:在圆桶轴线处放一直导线,在导线与桶壁间加上的电压也等于U,形成沿半径方向的辐向电场,尘粒的运动方向如图乙所示.已知空气阻力与尘粒运动的速度成正比,即F阻=kv(k为一定值),假设每个尘粒的质量和带电荷量均相同,不计尘埃的重力,则( )
有同学想通过静电除尘的方法净化空气.她用玻璃圆桶密闭含灰尘的空气,圆桶的高和直径相等.方法一是:在圆桶顶面和底面间加上电压U,沿圆桶的轴线方向形成一个匀强电场,尘粒的运动方向如图甲所示;方法二是:在圆桶轴线处放一直导线,在导线与桶壁间加上的电压也等于U,形成沿半径方向的辐向电场,尘粒的运动方向如图乙所示.已知空气阻力与尘粒运动的速度成正比,即F阻=kv(k为一定值),假设每个尘粒的质量和带电荷量均相同,不计尘埃的重力,则( )| A. | 两种方法中尘粒最终一定都做匀速运动 | |
| B. | 两种方法下尘粒受到的电场力大小相等 | |
| C. | 电场对单个尘粒做功的最大值相等 | |
| D. | 乙容器中的尘粒不可能做匀速直线运动 |
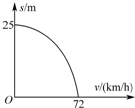 某司机在检测汽车性能过程中,得到汽车减速过程中的位移s与速度v的关系曲线如图所示,并得出位移s与速度v的函数关系式为s=m-nv2,其中m、n为常数.重力加速度的大小g取10m/s2.则以下判断正确的是( )
某司机在检测汽车性能过程中,得到汽车减速过程中的位移s与速度v的关系曲线如图所示,并得出位移s与速度v的函数关系式为s=m-nv2,其中m、n为常数.重力加速度的大小g取10m/s2.则以下判断正确的是( )| A. | 汽车在此过程中做匀变速直线运动 | |
| B. | 汽车的末速度为20m/s | |
| C. | 由题中所给已知条件可确定m、n的大小 | |
| D. | 汽车对司机作用力的大小与司机重力大小的比值为$\frac{4}{5}$ |
| A. | 熵增加原理说明一切自然过程总是向着分子热运动的无序性减小的方向进行 | |
| B. | 一定量100℃的水变成100℃的水蒸气,其分子之间的势能增加 | |
| C. | 气体如果失去容器的约束就会散开,这是因为气体分子之间存在斥力的缘故 | |
| D. | 一定质量的理想气体从外界吸收热量,其内能可能不变 | |
| E. | 水可以浸润玻璃,但是不能浸润石蜡,这个现象表明一种液体是否浸润某种固体与这两种物质的性质都有关系 |
| A. | 牛顿运动定律在宏观世界普遍适用 | |
| B. | 伽利略首先建立了描述运动所需要的物理概念,如平均速度,加速度等 | |
| C. | 在探究加速度、力和质量三者之间的关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系,这里运用了假设法 | |
| D. | 法拉第发现了法拉第电磁感应定律 |
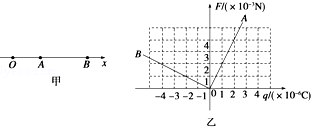
| A. | A点的电场强度大小为2×103N/C | B. | B点的电场强度大小为2×103N/C | ||
| C. | 点电荷Q在A、B之间 | D. | 点电荷Q在A、O之间 |

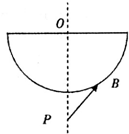 半圆柱玻璃体横截面如图所示.图中,O为玻璃截面的圆心,OP与水平直径垂直.一细激光束沿PB照射到半圆柱玻璃体上的B点,经半圆柱玻璃折射后,出射光线与OP平行.已知玻璃截面的圆半径为R,B到OP的距离为$\frac{R}{2}$,OP长为$\sqrt{3}$R.求玻璃体的折射率n.
半圆柱玻璃体横截面如图所示.图中,O为玻璃截面的圆心,OP与水平直径垂直.一细激光束沿PB照射到半圆柱玻璃体上的B点,经半圆柱玻璃折射后,出射光线与OP平行.已知玻璃截面的圆半径为R,B到OP的距离为$\frac{R}{2}$,OP长为$\sqrt{3}$R.求玻璃体的折射率n.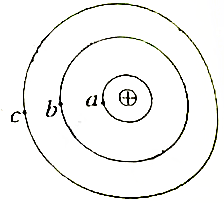 如图所示,a、b、c是氢原子的核外电子绕核运动的三个可能轨道,取无穷远电子的电势能为零,电子在a、b、c三个轨道时对应的电势能分别为-13.6eV、-3.4eV、-1.51eV,由于某种因素(如加热或光照)的影响,电子会沿椭圆轨道跃迁到离核更远的轨道上运动,求:
如图所示,a、b、c是氢原子的核外电子绕核运动的三个可能轨道,取无穷远电子的电势能为零,电子在a、b、c三个轨道时对应的电势能分别为-13.6eV、-3.4eV、-1.51eV,由于某种因素(如加热或光照)的影响,电子会沿椭圆轨道跃迁到离核更远的轨道上运动,求: