题目内容
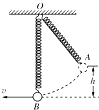
【题目】如图所示,一光滑的半径为R=1.6m的半圆形轨道放在水平面上,一个质量为m=2Kg的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,(1)求小球在最高点的速度?

(2)则小球落地点C距A处多远?
(3)当小球在最高点速度v=10m/s时对最高点的压力是多少?(g=10m/s2)
【答案】(1)4m/s (2)3.2m (3)105N
【解析】
(1)小球在恰好通过最高点时在最高点B只受重力作用,根据牛顿第二定律有:mg=![]()
可得小球在最高点的速度为:![]()
(2)小球离开B点开始做平抛运动,初速度为:v=4m/s,抛出点高度为:h=2R
则根据竖直方向做自由落体运动有:h=![]() gt2
gt2
可得小球做平抛运动的时间为:![]()
小球在水平方向做匀速直线运动,故平抛过程中小球在水平方向的位移为:x=vt=3.2m
(3)在最高点,根据牛顿第二定律可知:mg+FN=![]() ,
,
代入数据解得:FN=105N
根据牛顿第三定律可知对轨道的压力为105N

练习册系列答案
相关题目