题目内容
【题目】把沿x方向通有电流(x方向的电场强度为Ex)的长方体形的半导体材料,放在沿z方向的匀强磁场中,半导体材料的六个表面分别与相应的坐标平面平行;磁感应强度大小为Bx.在垂直于电场和磁场的+y或-y方向将产生一个横向电场Ey,这个现象称为霍尔效应,由霍尔效应产生的电场称为霍尔电场。实验表明霍尔电场Ey与电流的电流密度Jx和磁感应强度Bx的乘积成正比,即Ey=RHJxBz,比例系数RH称为霍尔系数。
某半导体材料样品中有两种载流子:空穴和电子;空穴和电子在单位电场下的平均速度(即载流子的平均速度与电场成正比的比例系数)分别为μp和-μn,空穴和电子的数密度分别为p和n,电荷分别为e和
一e.试确定该半导体材料的霍尔系数。
【答案】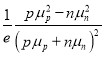
【解析】
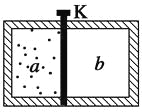
为确定起见,取坐标系如图所示,磁场沿Z方向,通电电流密度Jx沿x方向。设半导体材料中的载流子空穴和电子沿x方向的平均速率分别为vpx 和vnx,
由J=I/s,I=nqvs,得J=nqv
由题中已知条件知:空穴和电子的(单位体积内的)数密度为p和n;
故沿x方向的电流密度为
Jx=ep vpx +(-e)n(-vnx)
由题意知,其中 vpx=μpEx;-vnx=-μnEx
如果沿x方向的电流中只有一种载流子,则当作用于载流子的洛仑兹力与霍尔电场的作用力平衡时,霍尔电场达到稳定,如金属导体。
在半导体中,存在两种载流子,两种载流子受到的外磁场的洛仑兹力方向相同,受到的霍尔电场力方向相反,两种载流子受到的洛仑兹力不可能同时与霍尔电场力平衡,所以在半导体样品内存在载流子的横向流动,当任何时刻流向样品同一侧的空穴数与电子数相等时,霍尔电场便达到稳定。
(这段话讲述了半导体霍尔元件的工作机理,我比较浅显的理解是,①“当任何时刻流向样品同一侧的空穴数与电子数相等时”,这里空穴与电子在样品同一侧的流向是一致的,效果是相消的;②一开始空穴与电子在样品同一侧的流向是一致的,但数量是不相等的,比如一开始是空穴多,电子少;那么积累的电场不利于空穴的继续积累,而有利于电子的继续积累。但在这个阶段,霍尔电场在持续的增强。③同一侧的空穴数与电子数相等时,霍尔电场就稳定了!)
设两种载流子的横向平均速率分别为vpy 和vny,则横向电流密度为
Jy=ep(-vpy)+(-e)n(-vny)
这时,空穴在横向受到的作用力大小为:
Fpy=e[Ey-vpxBz]
这时的力是合力,其中[Ey-vpxBz]是等效合场强;
同理:电子在横向受到的作用力的大小为
Fny=(-e)[Ey-(-vnx)Bz]
其中[Ey-(-vnx)Bz]是等效合场强;
故两种载流子的横向平均速度为
-vpy=μp·Ey合=μp·[Ey-vpxBz]
-vny=-μp·E′y合=-μn·[Ey+vnxBz]
(个人粗浅的理解:个人觉得这个式子的得到与题中的表述是有一定差异的,题中说是“成正比”,“在单位电场下”,而这里却是用了一个等效的合场强)
霍尔电场达到稳定时有,Jy=0
综上各式
Ey=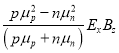
因为:Ey=RHJxBz
得霍尔系数
RH=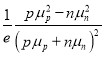
(注意:这里还要将Jx算出来,代进去)