题目内容
1. 质量为m的机车头拖着质量均为m的n节车厢在平直轨道上以速度v匀速行驶,行驶中后面有一节车厢脱落,待脱落车厢停止运动时后面又有一节车厢脱落,各节车厢按此方式依次脱落,整个过程中机车头的牵引力保持不变,求:全部车厢脱落并停止运动时机车头的速度大小为多少?
质量为m的机车头拖着质量均为m的n节车厢在平直轨道上以速度v匀速行驶,行驶中后面有一节车厢脱落,待脱落车厢停止运动时后面又有一节车厢脱落,各节车厢按此方式依次脱落,整个过程中机车头的牵引力保持不变,求:全部车厢脱落并停止运动时机车头的速度大小为多少?
分析 最后面一节车厢脱落后,根据牛顿第二定律求解机车头和剩下的车厢的加速度.
根据速度公式求出最后面一节车厢从脱落到停止运动的时间,再求解机车头和剩下的车厢的速度.
采用同样的方法求出第二节车厢脱离、第三节车厢脱离…等等停止运动时,机车头和剩下的车厢的速度,总结规律,得出全部车厢脱落并停止运动时,机车头的速度.
解答 解:设车头和车厢受到的摩擦力均为f,则匀速运动时的牵引力:F=(n+1)f,
最后面一节车厢脱落后,根据牛顿第二定律得机车头和剩下的车厢的加速度为:a1=$\frac{F-nf}{nm}$
联立得:a1=$\frac{f}{nm}$
最后面一节车厢脱落后,加速度大小为:a′=$\frac{f}{m}$
最后面一节车厢从脱落到停止运动的时间为:t1=$\frac{v}{a′}$=$\frac{mv}{f}$,
则当它停止运动时,机车头和剩下的车厢的速度为:v1=v+a1t1=v+$\frac{f}{nm}•\frac{mv}{f}$=$\frac{1+n}{n}v$
同理第二节车厢脱离后有:
v2=v1+a2t2=${v}_{1}+\frac{2f}{(n-1)m}$$•\frac{m{v}_{1}}{f}$=$\frac{(1+n){v}_{1}}{n-1}$=$\frac{(1+n)^{2}v}{n(n-1)}$
第三节车厢脱离:
v3=v2+a3t3=${v}_{2}+\frac{3f}{(n-2)m}$$•\frac{m{v}_{2}}{f}$=$\frac{(1+n){v}_{2}}{n-2}$=$\frac{(1+n)^{3}v}{n(n-1)(n-2)}$
…
根据数学归纳法,可得:vn=$\frac{(1+n)^{n}}{n(n-1)(n-2)…2•1}$=$\frac{(1+n)^{n}v}{n!}$
答:全部车厢脱落并停止运动时,机车头的速度是$\frac{(1+n)^{n}v}{n!}$.
点评 本题物理原理比较简单,关键在于运用数学归纳法寻找规律,考查运用数学知识处理物理问题的能力.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案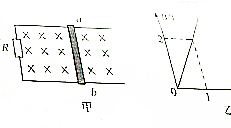 如图甲所示,水平放置的光滑金属导轨宽0.4m,金属棒ab距导轨左端也为0.4m,导轨与金属棒电阻不计,导轨左端电阻R=1Ω,导轨所围区域的磁场为匀强磁场,下列判断正确的是( )
如图甲所示,水平放置的光滑金属导轨宽0.4m,金属棒ab距导轨左端也为0.4m,导轨与金属棒电阻不计,导轨左端电阻R=1Ω,导轨所围区域的磁场为匀强磁场,下列判断正确的是( )| A. | 保持磁场B=0.5T不变,金属棒v=1m/s的速度向右匀速运动,则金属棒中电流I=0.5A | |
| B. | 金属棒静止,磁场按乙图变化,则金属棒中电流I=3.2A | |
| C. | 上述两种情况中,金属棒中电流方向都是a→b | |
| D. | 上述两种情况中,金属棒中电流方向都是b→a |
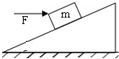 如图所示,一质量为m的物块在水平恒力F的作用下静止在粗糙的斜面上,若物块和斜面一直处于静止状态,下列说法中正确的是( )
如图所示,一质量为m的物块在水平恒力F的作用下静止在粗糙的斜面上,若物块和斜面一直处于静止状态,下列说法中正确的是( )| A. | 斜面对物块的作用力大小为$\sqrt{{F}^{2}+(mg)^{2}}$ | |
| B. | 物块一定受三个力作用 | |
| C. | 斜面与地面无摩擦力的作用 | |
| D. | 斜面与地面有摩擦力的作用,方向水平向左 |
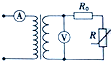 如图所示的电路中,变压器为理想变压器,原线圈接一正弦交变电流,副线圈接火灾报警系统(报警器未画出),电压表和电流表均为理想电表,R0为定值电阻,R为半导体热敏电阻,其阻值随温度的升高而减小,则当该装置附近有火源而导致其所在位置温度升高时(不考虑仪器的损坏)( )
如图所示的电路中,变压器为理想变压器,原线圈接一正弦交变电流,副线圈接火灾报警系统(报警器未画出),电压表和电流表均为理想电表,R0为定值电阻,R为半导体热敏电阻,其阻值随温度的升高而减小,则当该装置附近有火源而导致其所在位置温度升高时(不考虑仪器的损坏)( )| A. | 变压器的输出功率变大 | B. | 电压表的示数变大 | ||
| C. | R0的功率变小 | D. | 电流表的示数变小 |
 如图所示,在倾角为θ=30°的光滑斜面上,物块A、B质量分别为m和2m.物块A静止在轻弹簧上面,物块B用细线与斜面顶端相连,A、B紧挨在 但A、B之间无弹力.已知重力加速度为g,某时刻细线剪断,则细线剪断瞬间,下列说法错误的是( )
如图所示,在倾角为θ=30°的光滑斜面上,物块A、B质量分别为m和2m.物块A静止在轻弹簧上面,物块B用细线与斜面顶端相连,A、B紧挨在 但A、B之间无弹力.已知重力加速度为g,某时刻细线剪断,则细线剪断瞬间,下列说法错误的是( )| A. | 物块B的加速度为$\frac{1}{2}$g | B. | 物块A、B间的弹力为$\frac{1}{3}$mg | ||
| C. | 弹簧的弹力为$\frac{1}{2}$mg | D. | 物块A的加速度为$\frac{1}{3}$g |
 我国自行研制的动态测汽车尾气的装置中,包含有如图所示的部分装置,它由发射器和接收器两部分组成,安放在公路某车道两侧,汽车只能单方向鱼贯通过.发射器能垂直公路发出间隔均为d的三束激光,若不被汽车轮胎遮挡,都可以被接收器收到;若被挡住,可测出挡住相邻两光束的时间差△t.上述装置可以测出( )
我国自行研制的动态测汽车尾气的装置中,包含有如图所示的部分装置,它由发射器和接收器两部分组成,安放在公路某车道两侧,汽车只能单方向鱼贯通过.发射器能垂直公路发出间隔均为d的三束激光,若不被汽车轮胎遮挡,都可以被接收器收到;若被挡住,可测出挡住相邻两光束的时间差△t.上述装置可以测出( )| A. | 匀速运动时车的速度 | B. | 匀变速运动时车的加速度 | ||
| C. | 车的长度 | D. | 某时刻车的动能 |
| A. | 小物体带负电 | B. | 电场力对小物体做功为qEh | ||
| C. | 小物体的电势能增加了qEh | D. | 小物体的动能减少了qEh |
 一个表面光滑重为G的球放在斜面上,斜面倾角为α,有一不计厚度的木板挡住球,使球处于静止状态.今从图所示位置按逆时针方向缓慢转动木板到水平位置,则在此过程中,关于挡板对球的弹力大小变化说法正确的是( )
一个表面光滑重为G的球放在斜面上,斜面倾角为α,有一不计厚度的木板挡住球,使球处于静止状态.今从图所示位置按逆时针方向缓慢转动木板到水平位置,则在此过程中,关于挡板对球的弹力大小变化说法正确的是( )| A. | 一直变大 | B. | 一直变小 | C. | 先变大后变小 | D. | 先变小后变大 |