题目内容
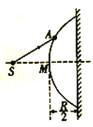
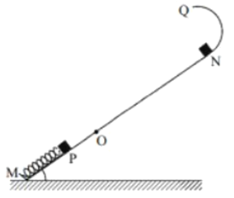
【题目】一光滑绝缘固定轨道MN与水平面成
角放置，其上端有一半径为l的光滑圆弧轨道的一部分，两轨道相切于N点，圆弧轨道末端Q点切线水平；一轻质弹簧下端固定在直轨道末端，弹簧原长时，其上端位于O点，
。现将一质量为m的滑块A拴接在弹簧上端，使之从O点静止释放。A向下压缩弹簧达到的最低点为P点，
。当A到达最低点P时，弹簧自动锁定，使A静止于P点。使质量也为m的滑块B，从N点由静止沿斜面下滑。B下滑至P点后，与A相碰，B接触A瞬间弹簧自动解锁，A、B碰撞时间极短内力远大于外力。碰后A、B有共同速度，但并不粘连。之后两滑块被弹回。（已知重力加速度为g，
，
）求：
(1)弹簧上端被压缩至P点时所具有的弹性势能；
(2)第一次碰撞过程中B对A弹力的冲量的大小；
(3)若要B最终恰能回到圆弧轨道最高点，需要在B滑块由N点出发时，给B多大的初速度。
【答案】(1)
(2)
(3)
【解析】
(1)A由O→P的过程
解得
(2)B由N→P的过程
A、B相碰的过程
以沿斜面向下为正方向
解得：
A对B的冲量大小为
(3)第二次B由N→P的过程
A、B相碰的过程
碰后，设A、B在弹簧压缩量为x处分离，对A、B
对B：
解得
即A、B在O点分离.
A、B碰后到弹簧恢复原长的过程
A、B分离后，到达的最高点Q点
解得
练习册系列答案
相关题目
