题目内容
13.地球的第一宇宙速度为v1,若某行星质量是地球质量的4倍,半径是地球半径的$\frac{1}{2}$倍,则该行星的第一宇宙速度2$\sqrt{2}$v1.分析 物体在地面附近绕地球做匀速圆周运动的速度叫做第一宇宙速度,大小7.9km/s,可根据卫星在圆轨道上运行时的速度公式v=$\sqrt{\frac{GM}{r}}$解得.
解答 解:设地球质量M,某星球质量4M,地球半径r,某星球半径0.5r;由万有引力提供向心力做匀速圆周运动得:
$\frac{GM}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$
解得卫星在圆轨道上运行时的速度公式为:v=$\sqrt{\frac{GM}{r}}$
分别代入地球和某星球的各物理量,解得:
v星球:v地球=$\sqrt{8}$:1
所以该行星的第一宇宙速度为2$\sqrt{2}$v1
故选:2$\sqrt{2}$v1.
点评 本题要掌握第一宇宙速度的定义,正确利用万有引力公式列出第一宇宙速度的表达式.

练习册系列答案
相关题目
4.工程师驾驶同一辆汽车以额定功率在A、B两种不同的路面上进行性能测试.汽车在路面A、B受到的阻力分别为fA、fB(fA>fB),最大速度分别为vA、vB,达到最大速度时的牵引力分别为FA、FB,则( )
| A. | vA<vB | B. | vA>vB | C. | FA=FB | D. | FA<FB |
8.一个质子与一个中子结合成一个氘核时释放2.2MeV的能量,两个中子和两个质子结合成一个氦核时,释放28.3MeV的能量.现在把两个中子和两个质子先结合成氘核,再把两个氘核结合成一个氦核,整个过程中释放的能量为( )
| A. | 不知氘核结合成氦核时释放的能量,无法判断 | |
| B. | 29.3MeV | |
| C. | 26.1MeV | |
| D. | 28.3MeV |
20.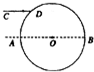 如图所示,真空中的匀质透明球体的半径为R,一束单色光沿方向平行于直径AB射向球体,入射角为60°,光线从D点射入球体经一次反射后由E(图中未标出)再次折射回真空中,此时的出射光线刚好与入射光线平行,已知光在真空中的速度为c.则( )
如图所示,真空中的匀质透明球体的半径为R,一束单色光沿方向平行于直径AB射向球体,入射角为60°,光线从D点射入球体经一次反射后由E(图中未标出)再次折射回真空中,此时的出射光线刚好与入射光线平行,已知光在真空中的速度为c.则( )
 如图所示,真空中的匀质透明球体的半径为R,一束单色光沿方向平行于直径AB射向球体,入射角为60°,光线从D点射入球体经一次反射后由E(图中未标出)再次折射回真空中,此时的出射光线刚好与入射光线平行,已知光在真空中的速度为c.则( )
如图所示,真空中的匀质透明球体的半径为R,一束单色光沿方向平行于直径AB射向球体,入射角为60°,光线从D点射入球体经一次反射后由E(图中未标出)再次折射回真空中,此时的出射光线刚好与入射光线平行,已知光在真空中的速度为c.则( )| A. | 该球体的绝对折射率为2 | |
| B. | 光线从D点射入到从E点射出球体的总时间为$\frac{6R}{c}$ | |
| C. | 从D点折射入球体的光线相对CD的偏折角为15° | |
| D. | 适当改变入射点的位置,光线进入球体后,可能会发生全反射 |

 由于条件所限,伽利略无法对自由落体运动进行准确实验研究.现在某同学在研究性学习中利用打点计时器针对自由落体运动进行深入研究,设计了如下实验方案:如图甲所示,将打点计时器固定在铁架台上,先打开电源,后释放重物,重物
由于条件所限,伽利略无法对自由落体运动进行准确实验研究.现在某同学在研究性学习中利用打点计时器针对自由落体运动进行深入研究,设计了如下实验方案:如图甲所示,将打点计时器固定在铁架台上,先打开电源,后释放重物,重物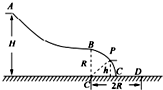 图为某游乐场内水上滑梯轨道示意图,整个轨道在同一竖直平面内,表面粗糙的AB段轨道与四分之一光滑圆弧轨道BC在B点水平相切,点A距水面的高度为H,圆弧轨道BC的半径为R.圆心O恰在水面,一质量为m的游客(视为质点)可从轨道AB上任意位置滑下,不计空气阻力.
图为某游乐场内水上滑梯轨道示意图,整个轨道在同一竖直平面内,表面粗糙的AB段轨道与四分之一光滑圆弧轨道BC在B点水平相切,点A距水面的高度为H,圆弧轨道BC的半径为R.圆心O恰在水面,一质量为m的游客(视为质点)可从轨道AB上任意位置滑下,不计空气阻力.