题目内容
18. 由于条件所限,伽利略无法对自由落体运动进行准确实验研究.现在某同学在研究性学习中利用打点计时器针对自由落体运动进行深入研究,设计了如下实验方案:如图甲所示,将打点计时器固定在铁架台上,先打开电源,后释放重物,重物
由于条件所限,伽利略无法对自由落体运动进行准确实验研究.现在某同学在研究性学习中利用打点计时器针对自由落体运动进行深入研究,设计了如下实验方案:如图甲所示,将打点计时器固定在铁架台上,先打开电源,后释放重物,重物带动纸带从静止开始下落,打出几条纸带并在其中选出一条比较理想的纸带如图乙所示,在纸带上取出若干计数点,其中每相邻计数点之间有四个点未画出,该同学已测得图中标出的数据s1、s2、s3、s4、s5,并已知打点计时器打点频率为f,需要计算重力加速度和打各点时的速度,计算重力加速度的公式是g=$\frac{s5-s2}{75}$f2(用f、s2、s5表示),计算打计数点5时重物速度的公式是v5=$\frac{2s5+s4-s3}{10}$f(用f、s3、s4、s5表示).
分析 根据连续相等时间内的位移之差是一恒量求出重力加速度,结合某段时间内的平均速度等于中间时刻的瞬时速度求出计数点4的瞬时速度,结合速度时间公式求出求出计数点5的速度.
解答 解:打点T=$\frac{5}{f}$,根据s5-s2=3gT2=$\frac{75g}{{f}^{2}}$ 得:
g=$\frac{{s}_{5}-{s}_{2}}{75}$f2.
计数点4的速度为:v4=$\frac{{s}_{4}+{s}_{5}}{2T}$=$\frac{{s}_{4}+{s}_{5}}{10}f$,
匀加速运动的加速度为:a=$\frac{{s}_{5}-{s}_{3}}{2{T}^{2}}$=$\frac{({s}_{5}-{s}_{3}){f}^{2}}{50}$,
则计数点5的速度为:v5=v4+aT=$\frac{2{s}_{5}+{s}_{4}-{s}_{3}}{10}$f.
故答案为:$\frac{s5-s2}{75}$f2,$\frac{2s5+s4-s3}{10}$f.
点评 解决本题的关键掌握纸带的处理,会通过纸带求解瞬时速度和加速度,关键是匀变速直线运动两个重要推论的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8. 如图为氢原子的能级图.现有大量的氢原子处于n=4的激发态,当向低能级跃迁时辐射出不同频率的光子.关于这些光子,下列说法正确的是( )
如图为氢原子的能级图.现有大量的氢原子处于n=4的激发态,当向低能级跃迁时辐射出不同频率的光子.关于这些光子,下列说法正确的是( )
 如图为氢原子的能级图.现有大量的氢原子处于n=4的激发态,当向低能级跃迁时辐射出不同频率的光子.关于这些光子,下列说法正确的是( )
如图为氢原子的能级图.现有大量的氢原子处于n=4的激发态,当向低能级跃迁时辐射出不同频率的光子.关于这些光子,下列说法正确的是( )| A. | 频率最大的光是由n=2的能级跃迁到n=1的能级产生的 | |
| B. | 释放出光子的最大能量为13.6eV | |
| C. | 这些氢原子总共可辐射出3种不同频率的光子 | |
| D. | 这些氢原子总共可辐射出6种不同频率的光子 |
6. 如图所示,在平面xy内有一沿水平x轴正方向传播的简谐横波,波速为3.0m/s,频率为2.5Hz,振幅为8.0×10-2m,已知t=0时刻P点质点的位移为y=4.0×10-2 m,速度沿y轴正方向,Q点在P点右方9.0×10-1m处,对于Q处的质点来说( )
如图所示,在平面xy内有一沿水平x轴正方向传播的简谐横波,波速为3.0m/s,频率为2.5Hz,振幅为8.0×10-2m,已知t=0时刻P点质点的位移为y=4.0×10-2 m,速度沿y轴正方向,Q点在P点右方9.0×10-1m处,对于Q处的质点来说( )
 如图所示,在平面xy内有一沿水平x轴正方向传播的简谐横波,波速为3.0m/s,频率为2.5Hz,振幅为8.0×10-2m,已知t=0时刻P点质点的位移为y=4.0×10-2 m,速度沿y轴正方向,Q点在P点右方9.0×10-1m处,对于Q处的质点来说( )
如图所示,在平面xy内有一沿水平x轴正方向传播的简谐横波,波速为3.0m/s,频率为2.5Hz,振幅为8.0×10-2m,已知t=0时刻P点质点的位移为y=4.0×10-2 m,速度沿y轴正方向,Q点在P点右方9.0×10-1m处,对于Q处的质点来说( )| A. | 在t=0时,位移为y=-4.0×10-2 m | |
| B. | 在t=0时,速度沿y轴负方向 | |
| C. | 在t=0.1 s时,位移为y=-4.0×10-2 m | |
| D. | 在t=0.1 s时,速度沿y轴正方向 |
1.下列说法正确的是( )
| A. | 如果物体(系统)所受到的合外力为零,则机械能一定守恒 | |
| B. | 如果合外力对物体(系统)做功为零,则机械能一定守恒 | |
| C. | 物体沿固定光滑曲面自由下滑过程中,不计空气阻力,机械能一定守恒 | |
| D. | 做匀速圆周运动的物体,其机械能一定守恒 |
8.某发电站采用高压输电向外输送电能.若输送的总功率为P0,输电电压为U,输电导线的总电阻为R,则下列说法正确的是( )
| A. | 输电线上的电流I=$\frac{U}{R}$ | B. | 输电线上的电流I=$\frac{{P}_{0}}{U}$ | ||
| C. | 输电线上损失的电压为U | D. | 输电线上损失的功率P=$\frac{{U}^{2}}{R}$ |
6.质量分别为m1和m2的两木块静止在水平面上,它们与水平面的动摩擦因数相同.在两木块上分别作用一水平力F1和F2,使它们在水平面上开始作匀加速运动,要使它们的动能达到E,F1和F2所必须做的功分别为W1和W2.下列说法正确的是( )
| A. | 若m1=m2,且F1>F2,则W1<W2 | B. | 若m1=m2,且F1>F2,则W1>W2 | ||
| C. | 若F1=F2,且m1>m2,则W1>W2 | D. | 若F1=F2,且m1>m2,则W1<W2 |
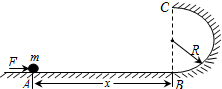 如图所示,光滑水平面右端B处连接一个竖直的半径为R的光滑半圆轨道,B点为水平面与轨道的切点,在离B距离为x的A点,用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力,质点沿半圆轨道运动到C处后又正好落回A点.试求:
如图所示,光滑水平面右端B处连接一个竖直的半径为R的光滑半圆轨道,B点为水平面与轨道的切点,在离B距离为x的A点,用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力,质点沿半圆轨道运动到C处后又正好落回A点.试求: 如图所示,A为有光滑曲面的固定轨道,轨道底端的切线方向是水平的,质量M=40kg的小车B静止于轨道右侧,其上表面与轨道底端在同一水平面上.一个质量m=20kg的物体C以2.0m/s的初速度从轨道顶端滑下,冲上小车B后经一段时间与小车相对静止并一起运动.若轨道顶端与底端的高度差h=1.6m.物体与小车板面间的动摩擦因数μ=0.40,小车与水平面间的摩擦忽略不计.(取g=10m/s2),求:
如图所示,A为有光滑曲面的固定轨道,轨道底端的切线方向是水平的,质量M=40kg的小车B静止于轨道右侧,其上表面与轨道底端在同一水平面上.一个质量m=20kg的物体C以2.0m/s的初速度从轨道顶端滑下,冲上小车B后经一段时间与小车相对静止并一起运动.若轨道顶端与底端的高度差h=1.6m.物体与小车板面间的动摩擦因数μ=0.40,小车与水平面间的摩擦忽略不计.(取g=10m/s2),求: