题目内容
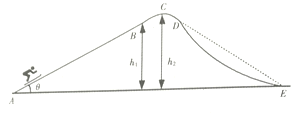
【题目】2018年平昌冬季运动会雪橇运动,其简化模型如图所示:倾角为
=37°的直线雪道AB与曲线雪道BCDE在B点平滑连接,其中A、E两点在同一水平面上,雪道最高点C所对应的圆弧半径R=10m,B、C两点距离水平面AE的高度分别为h1=18m与h2=20m,雪橇与雪道各处的动摩擦因数均为
=0.1,运动员可坐在电动雪橇上由A点从静止开始向上运动,若电动雪橇以恒定功率1.2KW工作10s后自动关闭,则雪橇和运动员(总质量m=50kg)到达C点的速度为2m/s,到达E点的速度为10m/s.已知雪橇运动过程中不脱离雪道且sin37°=0.6,cos37°=0.8,g=10m/s2,求:
(1)雪在C点时对雪道的压力;
(2)雪橇在BC段克服摩擦力所做的功;
(3)若仅将DE改成与曲线雪道CD平滑相接的倾斜直线雪道(如图中虚线所示),求雪橇
到E点时速度为多大?
【答案】(1)480N(2) 700J (3) 
【解析】（1）C点，雪橇和人由重力和支持力的合力提供向心力：
代入数据，得：FN=480N
由牛顿第三定律可知雪橇对轨道的压力大小为480N，方向竖直向下
（2）雪橇在段受AB到的滑动摩擦力为
.
从A到C根据动能定理：
解得：WBC=700J
（3）设CE的水平距离为x，从C到E点过程：
若是曲线轨道，克服摩擦力做的功为：
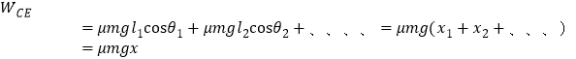
若是直线轨道，克服摩擦力做的功为：
..
故将DE改成倾斜直轨道，克服摩擦力做功不变，即损失的机械能也不变，则E点速度
综上所述本题答案是：(1)480N(2) 700J (3)
练习册系列答案
相关题目
