题目内容
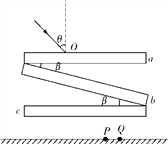
【题目】如图所示,在倾角为θ的没滑斜面上,有一长为![]() 的细线,细线的一端固定在O点,另一端拴一质量为m的小球现使小球恰好能在斜面上做完整的圆周运动,已知0点到斜面底边的距离 Soc=L,求:
的细线,细线的一端固定在O点,另一端拴一质量为m的小球现使小球恰好能在斜面上做完整的圆周运动,已知0点到斜面底边的距离 Soc=L,求:
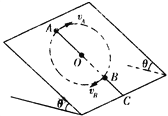
(1)小球通过最高点A时的速度vA;
(2)在最高点A和最低点B时细线上拉力之差
(3)小球运动到A点或B点时细线断裂,小球滑落到斜面底边时到C点的距离若相等,则![]() 和 L 应满足什么关系?
和 L 应满足什么关系?
【答案】(1)![]() (2)6mgsinθ(3)1.5l
(2)6mgsinθ(3)1.5l
【解析】试题分析:(1)小球恰好能在斜面上做完整的圆周运动,在A点时重力的下滑分量恰好提供向心力,列式即可求得![]() .(2)小球在最高点A和最低点B时分别运用牛顿第二定律列式,再运用机械能守恒得到最高点与最低点的速度,联立即可求得拉力之差(3)细线断裂后两球都做类平抛运动,结合类似平抛运动的知识求解l和L应满足的关系式.
.(2)小球在最高点A和最低点B时分别运用牛顿第二定律列式,再运用机械能守恒得到最高点与最低点的速度,联立即可求得拉力之差(3)细线断裂后两球都做类平抛运动,结合类似平抛运动的知识求解l和L应满足的关系式.
(1)小球恰好在斜面上做完整的圆周运动,则有:
![]()
解得:![]()
(2)在A点:![]()
在B点:![]()
由机械能守恒得:![]()
联立解得:![]()
(3)由(2)可求![]()
A点断裂:![]()
![]()
B点断裂:![]()
![]()
根据题意有:![]()
联立解得:![]()

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目