题目内容
【题目】如图所示,螺旋形光滑轨道竖直放置, P 、 Q 为对应的轨道最高点,一个小球以一定速度沿轨道切线方向进入轨道,且能过轨道最高点 P ,则下列说法中正确的是
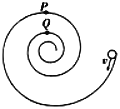
A. 轨道对小球做正功,小球的线速度移 vp> vQ
B. 轨道对小球不做功,小球的角速度 ωP< ωQ
C. 小球的向心加速度 aP> aQ
D. 轨道对小球的压力 FP> FQ
【答案】B
【解析】试题分析:轨道光滑,小球在运动的过程中只受重力和支持力,支持力时刻与运动方向垂直所以不做功,A错误;那么在整个过程中只有重力做功满足机械能守恒,根据机械能守恒有vP<vQ,在P、Q两点对应的轨道半径rP>rQ,根据![]() ,
,![]() ,得小球在P点的角速度小于在Q点的角速度,B正确;在P点的向心加速度小于在Q点的向心加速度,C错误;小球在P和Q两点的向心力由重力和支持力提供,即mg+FN=ma,可得P点对小球的支持力小于Q点对小球的支持力,D错。
,得小球在P点的角速度小于在Q点的角速度,B正确;在P点的向心加速度小于在Q点的向心加速度,C错误;小球在P和Q两点的向心力由重力和支持力提供,即mg+FN=ma,可得P点对小球的支持力小于Q点对小球的支持力,D错。

练习册系列答案
相关题目