题目内容
2.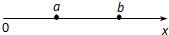 如图,一简谐横波在x轴上传播,轴上a、b两点相距12m.t=0时a点为波峰,b点为波谷;t=0.5s时,a点为波谷,b点为波峰.则下列判断中正确的是( )
如图,一简谐横波在x轴上传播,轴上a、b两点相距12m.t=0时a点为波峰,b点为波谷;t=0.5s时,a点为波谷,b点为波峰.则下列判断中正确的是( )| A. | 波一定沿x轴正方向传播 | B. | 波长可能是8m | ||
| C. | 周期可能是0.5s | D. | 波速可能是72m/s |
分析 本题中波的传播方向不确定,时间与周期的关系是不确定的,这样波长和周期也不确定,从而导致了波速的多解.根据两个质点的振动情况总是相反,平衡位置间的距离是半个波长的奇数倍,求波长的通项.根据时间是半个周期的奇数倍求周期的通项,从而得到波速的通项,再求特殊值.
解答 解:A、由题可知波的传播方向是不确定的,故A错误;
B、从波动图象可知:若a点为波峰,b点为波谷,则二者相距至少半个波长,或者n个波长另加半个波长,故有:xab=12m=(n+1212)λ,(n=0,1、2、3…),得 λ=242n+1242n+1m,当n=1时,λ=8m,故B正确;
C、由题有:t=0.5s=(k+1212) T,(k=0,1、2、3…),得 T=12k+112k+1s,k是整数,则T不可能是0.5s,故C错误.
D、波速为 v=λTλT=24(2k+1)2n+1m/s,(n、k=0,1、2、3…),当k=1,n=0时,v=72m/s,故D正确.
故选:BD
点评 本题考查了波的多解性,要知道造成多解性的原因:波长、周期多解性导致波速多解性,传播方向不确定造成多解性.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
7.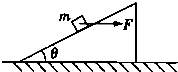 如图所示,质量为m的物块在倾角为θ的斜面上刚好匀速下滑,如果对物块施加一水平向右的外力F,物块刚好沿斜面向上匀速滑动,整个过程斜面保持静止不动,假设物块受到的最大静摩擦力等于滑动摩擦力,重力加速度为g,则下列说法正确的是( )
如图所示,质量为m的物块在倾角为θ的斜面上刚好匀速下滑,如果对物块施加一水平向右的外力F,物块刚好沿斜面向上匀速滑动,整个过程斜面保持静止不动,假设物块受到的最大静摩擦力等于滑动摩擦力,重力加速度为g,则下列说法正确的是( )
 如图所示,质量为m的物块在倾角为θ的斜面上刚好匀速下滑,如果对物块施加一水平向右的外力F,物块刚好沿斜面向上匀速滑动,整个过程斜面保持静止不动,假设物块受到的最大静摩擦力等于滑动摩擦力,重力加速度为g,则下列说法正确的是( )
如图所示,质量为m的物块在倾角为θ的斜面上刚好匀速下滑,如果对物块施加一水平向右的外力F,物块刚好沿斜面向上匀速滑动,整个过程斜面保持静止不动,假设物块受到的最大静摩擦力等于滑动摩擦力,重力加速度为g,则下列说法正确的是( )| A. | 当物体沿斜面向下刚好匀速下滑时斜面有向右的运动趋势 | |
| B. | 物体与斜面间的动摩擦因素是tanθ | |
| C. | 当物块沿斜面向上匀速滑行时,地面对斜面有向左的静摩擦力 | |
| D. | 当物块沿斜面向下匀速滑行时,斜面受到5个力作用 |
10.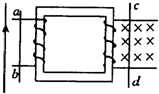 如图所示,ab和cd分别是放在变压器两测光滑水平导轨上的导体,cd静止.通电导线与ab在同一平面内( )
如图所示,ab和cd分别是放在变压器两测光滑水平导轨上的导体,cd静止.通电导线与ab在同一平面内( )
 如图所示,ab和cd分别是放在变压器两测光滑水平导轨上的导体,cd静止.通电导线与ab在同一平面内( )
如图所示,ab和cd分别是放在变压器两测光滑水平导轨上的导体,cd静止.通电导线与ab在同一平面内( )| A. | ab向右减速运动时,cd一定向左运动 | |
| B. | ab向右匀速运动时,cd不可能运动 | |
| C. | ab向右加速运动时,cd一定向左运动 | |
| D. | ab向右加速运动时,cd可能不动 |
7. 如图是某手机的充电器,将它接到220V的市电上能给手机提供5V的充电电压,说明该充电器内的变压器能够( )
如图是某手机的充电器,将它接到220V的市电上能给手机提供5V的充电电压,说明该充电器内的变压器能够( )
 如图是某手机的充电器,将它接到220V的市电上能给手机提供5V的充电电压,说明该充电器内的变压器能够( )
如图是某手机的充电器,将它接到220V的市电上能给手机提供5V的充电电压,说明该充电器内的变压器能够( )| A. | 升高交流电压 | B. | 降低交流电压 | C. | 升高直流电压 | D. | 降低直流电压 |
14. 如图所示,实线为某匀强电场的电场线,虚线为等势面,一个正电荷在等势面3时,动能为Ek3=20J,运动到1时,Ek1=4J,若以2为零势面,且不计空气阻力和重力,则当电荷的电势能Ep=4J 时,其动能为( )
如图所示,实线为某匀强电场的电场线,虚线为等势面,一个正电荷在等势面3时,动能为Ek3=20J,运动到1时,Ek1=4J,若以2为零势面,且不计空气阻力和重力,则当电荷的电势能Ep=4J 时,其动能为( )
 如图所示,实线为某匀强电场的电场线,虚线为等势面,一个正电荷在等势面3时,动能为Ek3=20J,运动到1时,Ek1=4J,若以2为零势面,且不计空气阻力和重力,则当电荷的电势能Ep=4J 时,其动能为( )
如图所示,实线为某匀强电场的电场线,虚线为等势面,一个正电荷在等势面3时,动能为Ek3=20J,运动到1时,Ek1=4J,若以2为零势面,且不计空气阻力和重力,则当电荷的电势能Ep=4J 时,其动能为( )| A. | Ek=10 J | B. | Ek=16 J | C. | Ek=4 J | D. | Ek=8 J |
11.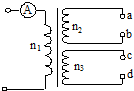 如图所示,变压器输入电压U一定,两个副线圈的匝数分别为n2和n3.当把电热器接在a、b上,使c、d空载时,通过原线圈中的电流表的示数是I0;当把同一电热器接在c、d上,使a、b空载时,电流表的示数为I′,则I0I′为( )
如图所示,变压器输入电压U一定,两个副线圈的匝数分别为n2和n3.当把电热器接在a、b上,使c、d空载时,通过原线圈中的电流表的示数是I0;当把同一电热器接在c、d上,使a、b空载时,电流表的示数为I′,则I0I′为( )
 如图所示,变压器输入电压U一定,两个副线圈的匝数分别为n2和n3.当把电热器接在a、b上,使c、d空载时,通过原线圈中的电流表的示数是I0;当把同一电热器接在c、d上,使a、b空载时,电流表的示数为I′,则I0I′为( )
如图所示,变压器输入电压U一定,两个副线圈的匝数分别为n2和n3.当把电热器接在a、b上,使c、d空载时,通过原线圈中的电流表的示数是I0;当把同一电热器接在c、d上,使a、b空载时,电流表的示数为I′,则I0I′为( )| A. | n2:n3 | B. | n3:n2 | C. | n22:n32 | D. | n32:n22 |
12.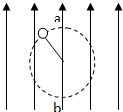 如图,在竖直向上的匀强电场中,一根不可伸长的绝缘细绳的一端系着一个带电小球,另一端固定于O点,小球在竖直平面内做匀速圆周运动,最高点为a,最低点为b,不计空气阻力,则( )
如图,在竖直向上的匀强电场中,一根不可伸长的绝缘细绳的一端系着一个带电小球,另一端固定于O点,小球在竖直平面内做匀速圆周运动,最高点为a,最低点为b,不计空气阻力,则( )
 如图,在竖直向上的匀强电场中,一根不可伸长的绝缘细绳的一端系着一个带电小球,另一端固定于O点,小球在竖直平面内做匀速圆周运动,最高点为a,最低点为b,不计空气阻力,则( )
如图,在竖直向上的匀强电场中,一根不可伸长的绝缘细绳的一端系着一个带电小球,另一端固定于O点,小球在竖直平面内做匀速圆周运动,最高点为a,最低点为b,不计空气阻力,则( )| A. | 小球带正电 | |
| B. | 电场力跟重力平衡 | |
| C. | 小球在从a运动到b的过程中,电势能增加 | |
| D. | 小球在运动过程中机械能守恒 |
 图为远距离输电示意图,两变压器均为理想变压器,升压变压器T的原、副线圈匝数比为n1:n2=1:100.在T的原线圈两端接入一电压u=100
图为远距离输电示意图,两变压器均为理想变压器,升压变压器T的原、副线圈匝数比为n1:n2=1:100.在T的原线圈两端接入一电压u=100