题目内容
14. 风洞实验室能产生大小和方向均可改变的风力.如图所示,在风洞实验室中有足够大的光滑水平面,在水平面上建立xOy直角坐标系.质量m=0.5kg的小球以初速度v0=0.40m/s从0点沿x轴正方向运动,在0~2.0s内受到一个沿y轴正方向、大小F1=0.20N的风力作用,小球运动2.0s后风力方向变为y轴负方向、大小变为F2=0.10N(图中未画出).试求:
风洞实验室能产生大小和方向均可改变的风力.如图所示,在风洞实验室中有足够大的光滑水平面,在水平面上建立xOy直角坐标系.质量m=0.5kg的小球以初速度v0=0.40m/s从0点沿x轴正方向运动,在0~2.0s内受到一个沿y轴正方向、大小F1=0.20N的风力作用,小球运动2.0s后风力方向变为y轴负方向、大小变为F2=0.10N(图中未画出).试求:(1)2.0s末小球在y方向的速度大小;
(2)2.0s内运动的位移大小;
(3)风力F2作用多长时间,小球的速度变为与初速度相同.
分析 (1)小球受重力、支持力和风的推力,在x方向不受外力,做匀速直线运动,在y方向受到恒定的力,故y方向做匀变速直线运动,根据运动的合成与分解的知识进行分析计算;
(2)根据位移时间公式求出分位移大小,再进行合成.
(3)当y方向的分速度减为零时,小球的速度变为与初速度相同,根据运动学公式列式求解即可.
解答 解:(1)小球受重力、支持力和风的推力,在x方向不受外力,做匀速直线运动,在y方向受到恒定的力,故y方向做匀变速直线运动;
设在0~2.0s内小球运动的加速度为a1,则根据牛顿第二定律,有 F1=ma1
解得:a1=$\frac{{F}_{1}}{m}$=$\frac{0.2}{0.5}$=0.4m/s2;
根据运动学公式,2.0s末小球在y方向的速度大小为:vy=a1t=0.80m/s
(2)2s内小球沿y方向的分位移为:Sy=$\frac{1}{2}$a1t2=0.80m
x方向的位移为:Sx=v0t=0.80m
故合位移为:S=$\sqrt{{S}_{x}^{2}+{S}_{y}^{2}}$=0.8$\sqrt{2}$≈1.13m
即2.0s内运动的位移大小为1.13m.
(3)根据牛顿第二定律,风力F2作用时物体的加速度为:
a2=$\frac{{F}_{2}}{m}$=$\frac{0.1}{0.5}$=0.20m/s2
风力F2作用时间为:t=$\frac{{v}_{y}}{{a}_{2}}$=$\frac{0.8}{0.2}$s=4.0s
故风力F2作用4s的时间,小球的速度变为与初速度相同.
答:(1)2.0s末小球在y方向的速度大小为0.80m/s;
(2)2.0s内运动的位移大小是1.13m;
(3)风力F2作用4s时间,小球的速度变为与初速度相同.
点评 本题关键要将小球的运动沿着x、y方向正交分解,x方向做匀速直线运动,y方向做匀变速直线运动,然后根据运动学公式进行列式求解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1、2、3轨道上正常运行时,以下说法正确的是( )
发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1、2、3轨道上正常运行时,以下说法正确的是( )| A. | 卫星在轨道3上的速率大于在轨道1上的速率 | |
| B. | 卫星在轨道3上的角速度小于在轨道1上的角速度 | |
| C. | 卫星在轨道1和3上运行时机械能守恒,在轨道2上运行时机械能不守恒 | |
| D. | 卫星在轨道2上经过P点时的加速度等于它在轨道3上经过P点时的加速度 |
| A. | 重力势能减少了mgh | B. | 动能减少了Fh | ||
| C. | 机械能减少了Fh | D. | 机械能减少了(F-mg)h |
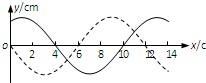 图中实线是沿x轴传播的一列简谐横波在t=0时刻的波形图,虚线是这列波在t=0.05s时刻的波形图.已知该波的波速是80cm/s,则下列说法中正确的是( )
图中实线是沿x轴传播的一列简谐横波在t=0时刻的波形图,虚线是这列波在t=0.05s时刻的波形图.已知该波的波速是80cm/s,则下列说法中正确的是( )| A. | 这列波有可能沿x轴正向传播 | |
| B. | 这列波的波长是12cm | |
| C. | 这列波的周期是0.15s | |
| D. | t=0.05s时刻x=6cm处的质点正在向上运动 |
 半径为r的带缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定放置的平行金属板连接,两板间距为d,如图甲所示.圆环内有一变化的磁场垂直于纸面,规定垂直纸面向里的方向为正,变化规律如图乙所示.在t=0时刻平行板之间的中心位置有一电荷量为+q的粒子由静止释放,粒子的重力不计,平行板电容器的充、放电时间不计,取上板的电势为零.则以下说法中正确的是( )
半径为r的带缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定放置的平行金属板连接,两板间距为d,如图甲所示.圆环内有一变化的磁场垂直于纸面,规定垂直纸面向里的方向为正,变化规律如图乙所示.在t=0时刻平行板之间的中心位置有一电荷量为+q的粒子由静止释放,粒子的重力不计,平行板电容器的充、放电时间不计,取上板的电势为零.则以下说法中正确的是( )| A. | 第2s末粒子回到了原来位置 | |
| B. | 第3s内上极板为正极 | |
| C. | 第2s末两极板之间的电场强度大小为$\frac{π{r}^{2}}{10d}$(V/m) | |
| D. | t=3.4s时,下极板的电势为$\frac{π{r}^{2}}{20}$(V) |
 如图所示,小球原来紧压在竖直放置的轻弹簧的上端,撤去外力,直至小球刚好离开弹簧的过程中,小球( )
如图所示,小球原来紧压在竖直放置的轻弹簧的上端,撤去外力,直至小球刚好离开弹簧的过程中,小球( )| A. | 动能先增大后减小 | |
| B. | 增加的动能和重力势能之和,等于弹簧减少的弹性势能 | |
| C. | 动能和重力势能发生了变化,但机械能保持不变 | |
| D. | 最大动能大于弹簧的最大弹性势能 |

 如图甲所示,物块A,B的质量分别是mA=5kg和mB=8kg,用轻弹簧栓接相连放在光滑的水平地面上,物块B右侧与竖直墙相接触.另有一物块C从t=0时以一定速度向右运动,在t=4s时与物块A相碰,并立即与A粘在一起不再分开.物块C的v-t图象如图乙所示.求:
如图甲所示,物块A,B的质量分别是mA=5kg和mB=8kg,用轻弹簧栓接相连放在光滑的水平地面上,物块B右侧与竖直墙相接触.另有一物块C从t=0时以一定速度向右运动,在t=4s时与物块A相碰,并立即与A粘在一起不再分开.物块C的v-t图象如图乙所示.求: