题目内容
19. 半径为r的带缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定放置的平行金属板连接,两板间距为d,如图甲所示.圆环内有一变化的磁场垂直于纸面,规定垂直纸面向里的方向为正,变化规律如图乙所示.在t=0时刻平行板之间的中心位置有一电荷量为+q的粒子由静止释放,粒子的重力不计,平行板电容器的充、放电时间不计,取上板的电势为零.则以下说法中正确的是( )
半径为r的带缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定放置的平行金属板连接,两板间距为d,如图甲所示.圆环内有一变化的磁场垂直于纸面,规定垂直纸面向里的方向为正,变化规律如图乙所示.在t=0时刻平行板之间的中心位置有一电荷量为+q的粒子由静止释放,粒子的重力不计,平行板电容器的充、放电时间不计,取上板的电势为零.则以下说法中正确的是( )| A. | 第2s末粒子回到了原来位置 | |
| B. | 第3s内上极板为正极 | |
| C. | 第2s末两极板之间的电场强度大小为$\frac{π{r}^{2}}{10d}$(V/m) | |
| D. | t=3.4s时,下极板的电势为$\frac{π{r}^{2}}{20}$(V) |
分析 由图可知磁感应强度的变化,则由楞次定则可得出平行板上的带电情况;对带电粒子受力分析可知带电粒子的受力情况,由牛顿第二定律可知粒子的运动情况;根据粒子受力的变化可知粒子加速度的变化,通过分析可得出粒子的运动过程.
解答 解:A、由楞次定律可知,在第1秒内,下板为正,粒子向下做匀加速运动,第2秒内,上板为正,粒子向下做匀减速运动,直到速度为零,第3秒内,上板为正,粒子向上做匀加速运动,第4秒内,下板为正,粒子向上做匀减速运动,直到速度为零回到原来位置,故A错误;
B、由图象可知,在第2秒内,磁场垂直于纸面向内,磁感应强度变小,穿过金属圆环的磁通量变小,假设闭合,由楞次定律可知,感应电流磁场与原磁场方向相同,即感应电流磁场方向垂直于纸面向内,然后由安培定则可知,感应电流沿顺时针方向,由此可见,上极板电势高,是正极,故B正确;
C、法拉第电磁感应定律可知,在第2秒内产生的感应电动势,E=$\frac{△∅}{△t}$=$\frac{△B}{△t}$S=πr2$\frac{0.1-0}{1}$=$\frac{π{r}^{2}}{10}$V,两极板间的电场强度为:E=$\frac{{E}_{电动势}}{d}$=$\frac{π{r}^{2}}{10d}$V/m,故C正确;
D、第4秒末下极板是正极,且粒子回到两板中点,因上板电势为零,则中点的电势为U=E×$\frac{d}{2}$=$\frac{π{r}^{2}}{20}$V,故D错误;
故选:BC.
点评 本题属于综合性题目,注意将产生感应电流的部分看作电源,则可知电容器两端的电压等于线圈两端的电压,这样即可还原为我们常见题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列关于运动和力的叙述中,正确的是( )
| A. | 若物体做匀速圆周运动,则其所受的合力一定指向圆心 | |
| B. | 若物体做曲线运动,则其所受的合力一定是变化的 | |
| C. | 若物体所受合力方向与运动方向相反,则其可能做曲线运动 | |
| D. | 若物体运动的速率在增加,则其所受合力与运动方向可能相反 |
10. 如图所示,在水平面和竖直墙壁之间放置质量为m、高为h的木块A和质量为M、半径为R的球B,各接触面均光滑,木块A受到水平向右的外力F作用,系统处于静止状态.O为B的球心,C为A、B接触点,CO与竖直方向夹角θ=60°.现撤去水平外力F,则( )
如图所示,在水平面和竖直墙壁之间放置质量为m、高为h的木块A和质量为M、半径为R的球B,各接触面均光滑,木块A受到水平向右的外力F作用,系统处于静止状态.O为B的球心,C为A、B接触点,CO与竖直方向夹角θ=60°.现撤去水平外力F,则( )
 如图所示,在水平面和竖直墙壁之间放置质量为m、高为h的木块A和质量为M、半径为R的球B,各接触面均光滑,木块A受到水平向右的外力F作用,系统处于静止状态.O为B的球心,C为A、B接触点,CO与竖直方向夹角θ=60°.现撤去水平外力F,则( )
如图所示,在水平面和竖直墙壁之间放置质量为m、高为h的木块A和质量为M、半径为R的球B,各接触面均光滑,木块A受到水平向右的外力F作用,系统处于静止状态.O为B的球心,C为A、B接触点,CO与竖直方向夹角θ=60°.现撤去水平外力F,则( )| A. | 撤去外力F瞬间,木块A的加速度aA<$\frac{F}{m}$ | |
| B. | 撤去外力F瞬间,球B的加速度aB=0 | |
| C. | 撤去外力F瞬间,墙壁对球B的弹力FB=0 | |
| D. | 若球B着地前瞬间速度为υ,则此时木块速度为$\sqrt{\frac{M}{m}(2gh-gR-{υ^2})}$ |
4. 如图甲为一列沿x轴传播的简谐波在t=O.1s时刻的波形图,图乙表示该波传播的介质中x=2m处的质点a从t=0时起的振动图象.则( )
如图甲为一列沿x轴传播的简谐波在t=O.1s时刻的波形图,图乙表示该波传播的介质中x=2m处的质点a从t=0时起的振动图象.则( )
 如图甲为一列沿x轴传播的简谐波在t=O.1s时刻的波形图,图乙表示该波传播的介质中x=2m处的质点a从t=0时起的振动图象.则( )
如图甲为一列沿x轴传播的简谐波在t=O.1s时刻的波形图,图乙表示该波传播的介质中x=2m处的质点a从t=0时起的振动图象.则( )| A. | 波传播的速度为20m/s | |
| B. | 波沿x轴正方向传播 | |
| C. | 波沿x轴负方向传播 | |
| D. | t=0.15s时,质点a的加速度沿y轴负方向 | |
| E. | t=0.15s时,x=4m处的质点b的加速度沿y轴正方向 |
11. 据报道,嫦娥二号探月卫星于2010年发射,其环月飞行的高度距离月球表面100km,所探测到的有关月球的数据将比环月飞行高度为200km的嫦娥一号更加详实.若两颗卫星环月运行均可视为匀速圆周运动,运行轨道如图所示.则( )
据报道,嫦娥二号探月卫星于2010年发射,其环月飞行的高度距离月球表面100km,所探测到的有关月球的数据将比环月飞行高度为200km的嫦娥一号更加详实.若两颗卫星环月运行均可视为匀速圆周运动,运行轨道如图所示.则( )
 据报道,嫦娥二号探月卫星于2010年发射,其环月飞行的高度距离月球表面100km,所探测到的有关月球的数据将比环月飞行高度为200km的嫦娥一号更加详实.若两颗卫星环月运行均可视为匀速圆周运动,运行轨道如图所示.则( )
据报道,嫦娥二号探月卫星于2010年发射,其环月飞行的高度距离月球表面100km,所探测到的有关月球的数据将比环月飞行高度为200km的嫦娥一号更加详实.若两颗卫星环月运行均可视为匀速圆周运动,运行轨道如图所示.则( )| A. | 嫦娥二号环月运行的周期比嫦娥一号更长 | |
| B. | 嫦娥二号环月运行时向心加速度比嫦娥一号更大 | |
| C. | 嫦娥二号环月运行时角速度比嫦娥一号更大 | |
| D. | 嫦娥二号环月运行时线速度大于月球的第一宇宙速度 |
9.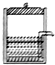 图示是压力保温瓶的结构简图,活塞a与液面之间密闭了一段质量的气体.假设封闭气体为理想气体且与外界没有热交换,则向下压a的过程中,瓶内气体( )
图示是压力保温瓶的结构简图,活塞a与液面之间密闭了一段质量的气体.假设封闭气体为理想气体且与外界没有热交换,则向下压a的过程中,瓶内气体( )
 图示是压力保温瓶的结构简图,活塞a与液面之间密闭了一段质量的气体.假设封闭气体为理想气体且与外界没有热交换,则向下压a的过程中,瓶内气体( )
图示是压力保温瓶的结构简图,活塞a与液面之间密闭了一段质量的气体.假设封闭气体为理想气体且与外界没有热交换,则向下压a的过程中,瓶内气体( )| A. | 内能增大 | B. | 体积增大 | ||
| C. | 压强增大 | D. | 温度升高 | ||
| E. | 分子间作用力增大 |
 一只小灯泡,标有“3V、0.6W”字样.现用图中给出的器材测量该小灯泡正常发光时的电阻Rx.(滑动变阻器最大阻值为10Ω;电源电动势为12V,内阻为1Ω;电流表内阻为1Ω;电压表的内阻为l0kΩ).
一只小灯泡,标有“3V、0.6W”字样.现用图中给出的器材测量该小灯泡正常发光时的电阻Rx.(滑动变阻器最大阻值为10Ω;电源电动势为12V,内阻为1Ω;电流表内阻为1Ω;电压表的内阻为l0kΩ). 风洞实验室能产生大小和方向均可改变的风力.如图所示,在风洞实验室中有足够大的光滑水平面,在水平面上建立xOy直角坐标系.质量m=0.5kg的小球以初速度v0=0.40m/s从0点沿x轴正方向运动,在0~2.0s内受到一个沿y轴正方向、大小F1=0.20N的风力作用,小球运动2.0s后风力方向变为y轴负方向、大小变为F2=0.10N(图中未画出).试求:
风洞实验室能产生大小和方向均可改变的风力.如图所示,在风洞实验室中有足够大的光滑水平面,在水平面上建立xOy直角坐标系.质量m=0.5kg的小球以初速度v0=0.40m/s从0点沿x轴正方向运动,在0~2.0s内受到一个沿y轴正方向、大小F1=0.20N的风力作用,小球运动2.0s后风力方向变为y轴负方向、大小变为F2=0.10N(图中未画出).试求: 如图所示,质量M=6kg上表面光滑的足够长木板,在水平拉力F=30N作用下,以v0=5m/s的初速度沿水平地面向右匀速运动.现有足够多的小铁块,它们的质量均为m=1kg,每当木板运动了L=1m时,就无初速度地在木板最右端放上一个铁块.g取10m/s2.求:
如图所示,质量M=6kg上表面光滑的足够长木板,在水平拉力F=30N作用下,以v0=5m/s的初速度沿水平地面向右匀速运动.现有足够多的小铁块,它们的质量均为m=1kg,每当木板运动了L=1m时,就无初速度地在木板最右端放上一个铁块.g取10m/s2.求: