题目内容
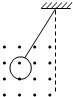
10. 如图所示,质量为m,电荷量为+q的粒子沿OD方向垂直进入一个以O为中心的圆形区域的匀强磁场B中,从该磁场穿出后又打在与磁场圆相切的屏上的P点,知PD:OD=$\sqrt{3}$:1,则粒子在磁场中运动的时间是多少?(不计重力)
如图所示,质量为m,电荷量为+q的粒子沿OD方向垂直进入一个以O为中心的圆形区域的匀强磁场B中,从该磁场穿出后又打在与磁场圆相切的屏上的P点,知PD:OD=$\sqrt{3}$:1,则粒子在磁场中运动的时间是多少?(不计重力)
分析 根据PD和OD的关系得出粒子的偏转角,抓住偏转角等于圆心角,结合周期公式求出粒子在磁场中的运动周期.
解答 解:因为PD:OD=$\sqrt{3}$:1,由几何关系知,∠POD=60°,
则粒子在磁场中的圆心角为60°.
则粒子在磁场中的运动时间t=$\frac{θ}{2π}T$=$\frac{1}{6}T=\frac{1}{6}×\frac{2πm}{qB}=\frac{πm}{3qB}$.
答:粒子在磁场中运动的时间为$\frac{πm}{3qB}$.
点评 解决本题的关键掌握粒子在磁场中的周期公式,知道求解运动时间的方法:1、根据t=$\frac{rθ}{v}$进行求解,θ为圆心角,2、根据$t=\frac{θ}{2π}T$进行求解.

练习册系列答案
相关题目
1.关于打点计时器打出的纸带,下列叙述正确的是( )
| A. | 必须从第一个点开始选取纸带 | |
| B. | 可以根据情况选取点迹清晰的部分纸带 | |
| C. | 选取的第一个点记为1,到第n个点的时间间隔为0.02ns | |
| D. | 选取的第一个点记为1,到第n个点的时间间隔为0.02(n-1)s |
15. 将一个闭合金属环用丝线悬于O点,如图所示.虚线左边有垂直于纸面向外的匀强磁场,而右边没有磁场.下列的现象能够发生的是( )
将一个闭合金属环用丝线悬于O点,如图所示.虚线左边有垂直于纸面向外的匀强磁场,而右边没有磁场.下列的现象能够发生的是( )
 将一个闭合金属环用丝线悬于O点,如图所示.虚线左边有垂直于纸面向外的匀强磁场,而右边没有磁场.下列的现象能够发生的是( )
将一个闭合金属环用丝线悬于O点,如图所示.虚线左边有垂直于纸面向外的匀强磁场,而右边没有磁场.下列的现象能够发生的是( )| A. | 金属环的摆动不会停下来,一直做等幅摆动 | |
| B. | 金属环的摆动幅度越来越小,小到某一数值后做等幅摆动 | |
| C. | 金属环的摆动会很快停下来 | |
| D. | 金属环最后一次向左摆动时,最终停在平衡位置左侧某一点处 |
4. 如图所示,甲带负电,乙是足够长的不带电的绝缘木板,甲、乙叠放在一起置于粗糙的地板上,空间有垂直纸面向里的匀强磁场,用水平恒力F拉乙物块,使甲、乙从静止开始向左运动,在甲运动达到稳态的过程中( )
如图所示,甲带负电,乙是足够长的不带电的绝缘木板,甲、乙叠放在一起置于粗糙的地板上,空间有垂直纸面向里的匀强磁场,用水平恒力F拉乙物块,使甲、乙从静止开始向左运动,在甲运动达到稳态的过程中( )
 如图所示,甲带负电,乙是足够长的不带电的绝缘木板,甲、乙叠放在一起置于粗糙的地板上,空间有垂直纸面向里的匀强磁场,用水平恒力F拉乙物块,使甲、乙从静止开始向左运动,在甲运动达到稳态的过程中( )
如图所示,甲带负电,乙是足够长的不带电的绝缘木板,甲、乙叠放在一起置于粗糙的地板上,空间有垂直纸面向里的匀强磁场,用水平恒力F拉乙物块,使甲、乙从静止开始向左运动,在甲运动达到稳态的过程中( )| A. | 甲、乙间的摩擦力不断增大 | B. | 甲、乙间的摩擦力不断减小 | ||
| C. | 甲、乙间摩擦力先增后减直至为零 | D. | 乙物块与地面间的摩擦力不断减小 |
 如图所示,一质子由静止经电压U0加速后,进入两块间距为d、电压为U的平行金属板之间,若质子从两板正中间垂直于电场方向射入,且刚好能从极板边缘穿出电场.试求:
如图所示,一质子由静止经电压U0加速后,进入两块间距为d、电压为U的平行金属板之间,若质子从两板正中间垂直于电场方向射入,且刚好能从极板边缘穿出电场.试求: 如图所示,只有在y>0的区域中,存在着垂直于纸面的、磁感应强度为B的匀强磁场,一个质量为m、带电量为q的带正电粒子(不计重力),从坐标原点O以初速度v0沿着与x轴正向成30°角的方向垂直于磁场方向进入.
如图所示,只有在y>0的区域中,存在着垂直于纸面的、磁感应强度为B的匀强磁场,一个质量为m、带电量为q的带正电粒子(不计重力),从坐标原点O以初速度v0沿着与x轴正向成30°角的方向垂直于磁场方向进入. ①用多用电表的欧姆挡测量阻值时,选择倍率为×10的欧姆挡,按正确的实验操作步骤测量,表盘指针位置如图所示,该电阻的阻值约为170Ω;
①用多用电表的欧姆挡测量阻值时,选择倍率为×10的欧姆挡,按正确的实验操作步骤测量,表盘指针位置如图所示,该电阻的阻值约为170Ω;