题目内容
20. 如图所示,一质子由静止经电压U0加速后,进入两块间距为d、电压为U的平行金属板之间,若质子从两板正中间垂直于电场方向射入,且刚好能从极板边缘穿出电场.试求:
如图所示,一质子由静止经电压U0加速后,进入两块间距为d、电压为U的平行金属板之间,若质子从两板正中间垂直于电场方向射入,且刚好能从极板边缘穿出电场.试求:(1)金属板的长度L;
(2)质子穿出电场时的动能.
分析 (1)质子进入偏转电场后做类平抛运动,沿水平方向做匀速直线运动,位移大小等于板长L;竖直方向做匀加速直线运动,位移大小等于板间距离的一半,由牛顿第二定律求出加速度,由运动学公式求解板长L.
(2)从刚开始到射出电场的过程中运用动能定理即可求出质子穿出电场时的动能
解答 解:(1)在加速过程根据动能定理得:
eU0=$\frac{1}{2}{mv}_{0}^{2}$
解得到质子射出加速电场的速度v0=$\sqrt{\frac{2e{U}_{0}}{m}}$
粒子在竖直方向:y=$\frac{d}{2}$=$\frac{1}{2}a{t}^{2}$,
又a=$\frac{eU}{md}$
在水平方向:x=L=v0t
联立上式得到$\frac{d}{2}=\frac{1}{2}×\frac{eU}{md}×(\frac{L}{{v}_{0}})^{2}$
代入数据得L=d$\sqrt{\frac{2{U}_{0}}{U}}$
(2)从刚开始到射出电场的过程中运用动能定理得:$\frac{1}{2}m{v}^{2}=e({U}_{0}+\frac{U}{2})$
答:(1)金属板的长L为d$\sqrt{\frac{2{U}_{0}}{U}}$;
(2)质子穿出电场时的动能(质子的电量为e)为e(U0+$\frac{U}{2}$);
点评 本题是组合场问题,关键是分析质子的分析情况和运动情况.在偏转电场中质子做类平抛运动,采用运动的分解方法研究

练习册系列答案
相关题目
10. 如图所示,A、B两物体的重力分别是GA=3N,GB=4N.A用细线悬挂在顶板上,B放在水平面上,A、B间轻弹簧中的弹力F=2N,则细线中的张力T及B对地面的压力N的可能值分别是( )
如图所示,A、B两物体的重力分别是GA=3N,GB=4N.A用细线悬挂在顶板上,B放在水平面上,A、B间轻弹簧中的弹力F=2N,则细线中的张力T及B对地面的压力N的可能值分别是( )
 如图所示,A、B两物体的重力分别是GA=3N,GB=4N.A用细线悬挂在顶板上,B放在水平面上,A、B间轻弹簧中的弹力F=2N,则细线中的张力T及B对地面的压力N的可能值分别是( )
如图所示,A、B两物体的重力分别是GA=3N,GB=4N.A用细线悬挂在顶板上,B放在水平面上,A、B间轻弹簧中的弹力F=2N,则细线中的张力T及B对地面的压力N的可能值分别是( )| A. | 5 N和6 N | B. | 5 N和2 N | C. | 1 N和6 N | D. | 1 N和2 N |
5. 如图所示,匀强电场场强大小为E,方向与水平方向夹角为θ(θ≠45°),场中有一质量为m,电荷量为q的带电小球,用长为L的细线悬挂于O点,当小球静止时,细线恰好水平,现用一外力将小球沿圆弧缓慢拉到竖直方向最低点,小球电荷量不变,则在此过程中有( )
如图所示,匀强电场场强大小为E,方向与水平方向夹角为θ(θ≠45°),场中有一质量为m,电荷量为q的带电小球,用长为L的细线悬挂于O点,当小球静止时,细线恰好水平,现用一外力将小球沿圆弧缓慢拉到竖直方向最低点,小球电荷量不变,则在此过程中有( )
 如图所示,匀强电场场强大小为E,方向与水平方向夹角为θ(θ≠45°),场中有一质量为m,电荷量为q的带电小球,用长为L的细线悬挂于O点,当小球静止时,细线恰好水平,现用一外力将小球沿圆弧缓慢拉到竖直方向最低点,小球电荷量不变,则在此过程中有( )
如图所示,匀强电场场强大小为E,方向与水平方向夹角为θ(θ≠45°),场中有一质量为m,电荷量为q的带电小球,用长为L的细线悬挂于O点,当小球静止时,细线恰好水平,现用一外力将小球沿圆弧缓慢拉到竖直方向最低点,小球电荷量不变,则在此过程中有( )| A. | 外力所做的功为$\frac{mgL}{tanθ}$ | |
| B. | 带电小球的电势能增加qEL( sinθ+cosθ) | |
| C. | 带电小球的电势能增加$\frac{2mgL}{tanθ}$ | |
| D. | 外力所做的功为mgLtanθ |
12.甲、乙两个做匀速圆周运动的物体,它们的质量之比为2:3,半径之比为3:4,周期之比是1:2,则( )
| A. | 甲与乙的线速度之比为3:2 | B. | 甲与乙的角速度之比为3:2 | ||
| C. | 甲与乙的向心加速度之比为2:1 | D. | 甲与乙所受到的向心力之比为1:2 |
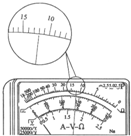 某人用多用电表按正确步骤测量一个电阻的阻值,当选择欧姆挡“×1”挡测量时,指针指示位置如图所示,则其电阻值是12.如果要用这支多用电表测量一个约200欧的电阻,为了使测量比较精确,选择开关应选的欧姆挡是×10.(填“×1”、“×10”或“×100”).
某人用多用电表按正确步骤测量一个电阻的阻值,当选择欧姆挡“×1”挡测量时,指针指示位置如图所示,则其电阻值是12.如果要用这支多用电表测量一个约200欧的电阻,为了使测量比较精确,选择开关应选的欧姆挡是×10.(填“×1”、“×10”或“×100”). 如图用细绳AO、BO悬挂重20N的重物,AO与竖直方向成30°,BO水平.求细绳 AO、BO对重物的拉力FA与FB.
如图用细绳AO、BO悬挂重20N的重物,AO与竖直方向成30°,BO水平.求细绳 AO、BO对重物的拉力FA与FB.

 如图所示,质量为m,电荷量为+q的粒子沿OD方向垂直进入一个以O为中心的圆形区域的匀强磁场B中,从该磁场穿出后又打在与磁场圆相切的屏上的P点,知PD:OD=$\sqrt{3}$:1,则粒子在磁场中运动的时间是多少?(不计重力)
如图所示,质量为m,电荷量为+q的粒子沿OD方向垂直进入一个以O为中心的圆形区域的匀强磁场B中,从该磁场穿出后又打在与磁场圆相切的屏上的P点,知PD:OD=$\sqrt{3}$:1,则粒子在磁场中运动的时间是多少?(不计重力)