题目内容
13. 让小球从斜面的顶端滚下,如图所示,图中标出了不同时刻小球沿斜面滚下的位置,试粗略计算:
让小球从斜面的顶端滚下,如图所示,图中标出了不同时刻小球沿斜面滚下的位置,试粗略计算:(1)小球从O到B的平均速度;
(2)小球在A点和B点的瞬时速度各为多少;
(3)小球运动的加速度大小.
分析 根据平均速度的定义式求出小球在O到B的平均速度,结合某段时间内的瞬时速度等于中间时刻的瞬时速度求出A、B的速度大小.根据连续相等时间内的位移之差是一恒量求出小球运动的加速度.
解答 解:(1)小球从O到B的平均速度$\overline{v}=\frac{x}{2T}=\frac{0.16}{0.2}m/s=0.8m/s$.
(2)小球在A点的瞬时速度等于OB段的平均速度,等于0.8m/s,
B点的瞬时速度等于AC的瞬时速度,则${v}_{B}=\frac{{x}_{AC}}{2T}=\frac{0.27-0.07}{0.2}m/s=1.0m/s$.
(3)根据△x=aT2得,小球运动的加速度a=$\frac{△x}{{T}^{2}}=\frac{[(16-7)-7]×1{0}^{-2}}{0.01}=2m/{s}^{2}$.
答:(1)小球从O到B的平均速度为 0.8m/s;
(2)小球在A点和B点的瞬时速度各为0.8m/s、1.0m/s;
(3)小球运动的加速度大小为2m/s2.
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,对于第三问,也可以根据瞬时速度,结合速度时间公式求出加速度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.以下是有关近代物理内容的若干叙述,其中正确的有( )
| A. | 紫外线照射到金属锌板表面时能产生光电效应,则当增大紫外线的照射强度时,从锌板表面逸出的光电子的最大初动能也随之增大 | |
| B. | 每个核子只跟邻近的核子发生核力作用 | |
| C. | 原子核式结构模型是由汤姆逊在a粒子散射实验基础上提出的 | |
| D. | 太阳内部发生的核反应是热核反应 | |
| E. | 关于原子核内部的信息,最早来自天然放射现象 |
4. 图中的甲是地球赤道上的一个物体,乙是“神舟十号”宇宙飞船(周期约90min),丙是地球的同步卫星,它们运行的轨道示意图如图所示,它们都绕地心做匀速圆周运动.下列有关说法中正确的是( )
图中的甲是地球赤道上的一个物体,乙是“神舟十号”宇宙飞船(周期约90min),丙是地球的同步卫星,它们运行的轨道示意图如图所示,它们都绕地心做匀速圆周运动.下列有关说法中正确的是( )
 图中的甲是地球赤道上的一个物体,乙是“神舟十号”宇宙飞船(周期约90min),丙是地球的同步卫星,它们运行的轨道示意图如图所示,它们都绕地心做匀速圆周运动.下列有关说法中正确的是( )
图中的甲是地球赤道上的一个物体,乙是“神舟十号”宇宙飞船(周期约90min),丙是地球的同步卫星,它们运行的轨道示意图如图所示,它们都绕地心做匀速圆周运动.下列有关说法中正确的是( )| A. | 它们运动的向心加速度大小关系是a乙>a丙>a甲 | |
| B. | 它们运动的线速度大小关系是v乙<v丙<v甲 | |
| C. | 已知甲运动的周期T甲=24h,可计算出地球的密度ρ=$\frac{3π}{G{T}_{甲}^{2}}$ | |
| D. | 已知乙运动的周期T乙及轨道半径r乙,可计算出地球质量M=$\frac{4{π}^{2}{r}_{乙}^{3}}{G{T}_{乙}^{2}}$ |
8.一物体做匀加速直线运动,加速度为2m/s2,这就是说( )
| A. | 物体速度变化量是2m/s | |
| B. | 每经过一秒物体的速度都增大2m/s | |
| C. | 任意一秒内的末速度均为初速度的2倍 | |
| D. | 第n s末的速度比第1s末的速度大2(n-1)m/s |
5. 如图所示,一物体自P点以初速度10m/s做平抛运动,恰好垂直打到倾角为45°的斜面上的Q点(g=10m/s2).则PQ两点间的距离为( )
如图所示,一物体自P点以初速度10m/s做平抛运动,恰好垂直打到倾角为45°的斜面上的Q点(g=10m/s2).则PQ两点间的距离为( )
 如图所示,一物体自P点以初速度10m/s做平抛运动,恰好垂直打到倾角为45°的斜面上的Q点(g=10m/s2).则PQ两点间的距离为( )
如图所示,一物体自P点以初速度10m/s做平抛运动,恰好垂直打到倾角为45°的斜面上的Q点(g=10m/s2).则PQ两点间的距离为( )| A. | 5m | B. | l0m | ||
| C. | 5$\sqrt{5}$m | D. | 条件不足,无法求解 |
2.下列说法中错误的是( )
| A. | 两个分运动是直线运动,则它们的合运动也一定是直线运动 | |
| B. | 两个分运动是匀速直线运动,则它们的合运动也一定是匀速直线运动 | |
| C. | 两个分运动是初速度为零的匀加速直线运动,则它们的合运动也一定是初速度为零的匀加速直线运动 | |
| D. | 两个分运动是初速度不为零的匀加速直线运动,则它们的合运动可能是匀加速曲线运动 |
 正常转动的时针、分针、秒针,都可视为匀速圆周运动,则它们的角速度之比为1:12:720;如果三针的长度之比是2:3:3,则三针针尖的线速度之比为1:18:1 080.
正常转动的时针、分针、秒针,都可视为匀速圆周运动,则它们的角速度之比为1:12:720;如果三针的长度之比是2:3:3,则三针针尖的线速度之比为1:18:1 080.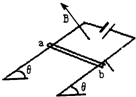 如图所示,在与水平面成θ角且连接电源的金属框架上,放一长为L,质量为M的金属杆ab,磁场的磁感应强度为B,方向垂直框架所在的平面,当金属杆中通有电流I时,它恰好沿金属框架向下匀速运动,求金属杆与金属框架之间的动摩擦因数.
如图所示,在与水平面成θ角且连接电源的金属框架上,放一长为L,质量为M的金属杆ab,磁场的磁感应强度为B,方向垂直框架所在的平面,当金属杆中通有电流I时,它恰好沿金属框架向下匀速运动,求金属杆与金属框架之间的动摩擦因数.