Question

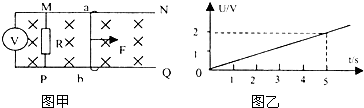
（19分）如图甲所示，光滑且足够长的平行金属导轨MN、PQ与水平面间的倾角=30°，两导轨间距L=0.3m。导轨电阻忽略不计，其间连接有阻值R=0.4Ω的固定电阻。开始时，导轨上固定着一质量m=0.1kg、电阻r=0.2Ω的金属杆ab，整个装置处于磁感应强度B=0.5T的匀强磁场中，磁场方向垂直导轨面向下。现拆除对金属杆ab的约束，同时用一平行金属导轨面的外力F沿斜面向上拉金属杆ab，使之由静止开始向上运动。电压采集器可将其两端的电压U即时采集并输入电脑，获得的电压U随时间t变化的关系如图乙所示。求：（1）在t=2.0s时通过金属杆的感应电流的大小和方向；（2）金属杆在2.0s内通过的位移；（3）2s末拉力F的瞬时功率。

 

Answer 1

【答案】

（1）0.5A，方向由a指向b

（2）2m

（3）1.35W

【解析】（1）由图象可知，当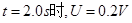，此时电路中的电流（即通过金属杆的电流）

                                                                2分

用右手定则判断出，此时电流的方向由a指向b                 1分

（2）由图象知U=kt=0.1t                                                 1分

金属杆切割磁场运动产生电磁感应电动势：E=BLv          1分

由电路分析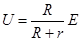：                                              1分

联立以上两式得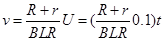：               1分

 

由于R、r、B及L均为常数，所以v与t成正比，即金属杆沿斜面向上方向做初速度为零的匀加速直线运动                             2分

匀加速运动的加速度为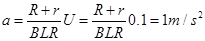       2分

则金属杆在2.0s内通过的位移：

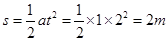                                             2分

（3）在第2s末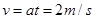，                             1分

杆受安培力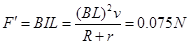                   2分

由牛顿第二定律，对杆有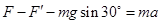              2分

解得：拉力F=0.675N故2s末拉力F的瞬时功率

P=Fv=1.35W  1分