题目内容
如图甲所示,光滑且足够长的平行金属导轨MN、PQ固定在同一水平面上,两导轨间距L=0.2m,电阻R=0.4Ω,导轨上停放一质量为m=0.1kg,电阻为r=0.1Ω的金属杆ab,导轨的电阻不计,整个装置处于磁感应强度为B=0.5T的匀强磁场中,磁场的方向竖直向下.现用一外力F沿水平方向拉杆,使之由静止开始运动,若理想电压表示数U随时间t的变化关系如图乙所示.
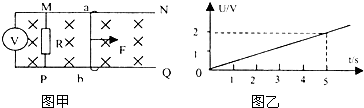
求:(1)运动速度随时间t的变化关系式;
(2)金属杆运动的加速度;
(3)第5秒末外力F的功率.

求:(1)运动速度随时间t的变化关系式;
(2)金属杆运动的加速度;
(3)第5秒末外力F的功率.
分析:先写出电动势的表达式,再根据U-t的图象,写出速度随时间的变化关系;通过速度随时间的变化关系和加速度的定义,求出加速度;根据瞬时功率的表达式,求出第5秒末外力F的功率.
解答:解:(1)、(2)导体棒上产生的电动势:E=BLv
电阻上的电流:I=
电压表上的电压:U=IR
故:v=
电压U=2V,t=5s时,代人数据,得;v=25m/s
金属杆的加速度:a=
=
=5m2/s
金属杆运动速度随时间t的变化关系式:v=0+at=5t
(3)金属杆上所受的安培力为:F安=BIL=
=0.5N
设外力的大小为F.
根据牛顿第二定律得:F-F安=ma
外力F的功率:P=Fv=(F安+ma)v=(0.5+0.1×5)×25W=25W
代人数据,解得:P=10W
答:(1)属杆运动速度随时间t的变化关系式:v=5t m/s;(2)金属杆的加速度5m2/s;(3)第5秒末外力F的功率25W.
电阻上的电流:I=
| E |
| R+r |
电压表上的电压:U=IR
故:v=
| U(R+r) |
| RBL |
电压U=2V,t=5s时,代人数据,得;v=25m/s
金属杆的加速度:a=
| △v |
| △t |
| v-0 |
| t-0 |
金属杆运动速度随时间t的变化关系式:v=0+at=5t
(3)金属杆上所受的安培力为:F安=BIL=
| B2L2v |
| R+r |
设外力的大小为F.
根据牛顿第二定律得:F-F安=ma
外力F的功率:P=Fv=(F安+ma)v=(0.5+0.1×5)×25W=25W
代人数据,解得:P=10W
答:(1)属杆运动速度随时间t的变化关系式:v=5t m/s;(2)金属杆的加速度5m2/s;(3)第5秒末外力F的功率25W.
点评:先写出电动势的表达式,再写出速度随时间的变化关系;由加速度的定义,求出加速度;根据瞬时功率的表达式,求出第5秒末外力F的功率.涉及的知识点较多,属于中档题目.

练习册系列答案
相关题目



