题目内容
12. 如图所示,一个半径为r的圆木板静止在水面上,在圆木板圆心O的正下方H=$\sqrt{3}$r处有一点光源S,已知水的折射率n=$\sqrt{2}$
如图所示,一个半径为r的圆木板静止在水面上,在圆木板圆心O的正下方H=$\sqrt{3}$r处有一点光源S,已知水的折射率n=$\sqrt{2}$ (1)求沿圆木板边缘出射的折射光线的折射角.
(2)若要在水面上方观察不到点光源S所发出的光,则应将点光源S至少竖直向上移多大的距离?(结果可用根式表示)
分析 (1)由几何关系求出光线射到圆木板边缘时的入射角,再由折射定律求解折射角即可.
(2)若要在水面上方观察不到点光源S所发出的光,光线在木板边缘要发生反射,由sinC=$\frac{1}{n}$求出临界角,再由几何知识解答即可.
解答  解:(1)如图,设光线射到圆木板边缘时的入射角为i,由几何知识得
解:(1)如图,设光线射到圆木板边缘时的入射角为i,由几何知识得
tani=$\frac{r}{H}$=$\frac{1}{\sqrt{3}}$,i=30°
由折射定律得 n=$\frac{sinr}{sini}$
则得 sinr=nsini=$\sqrt{2}$sin30°=$\frac{\sqrt{2}}{2}$
故折射角为 r=45°
(2)设临界角为C,当入射角i=C时光线在木板边缘要发生反射,在水面上方观察不到点光源S所发出的光.
由sinC=$\frac{1}{n}$=$\frac{1}{\sqrt{2}}$,得C=45°
由几何知识可得:点光源S竖直向上移的最小距离为 s=H-r=($\sqrt{3}$-1)r
答:(1)沿圆木板边缘出射的折射光线的折射角为45°.(2)应将点光源S至少竖直向上移($\sqrt{3}$-1)r的距离.
点评 对于有关全反射问题,关键是画出光路图,然后根据折射定律列式求解;要注意在运用折射定律n=$\frac{sini}{sinr}$时,要明确条件:光从真空射入介质.

练习册系列答案
相关题目
20.如图甲为小型旋转电枢式交流发电机的原理图,其矩形线圈在磁感应强度为B的匀强磁场中,绕垂直于磁场方向的固定轴OO′匀速转动,线圈的两端经集流环和电刷与电阻R=10Ω连接,与电阻R并联的交流电压表为理想电压表,示数是10V.图乙是矩形线圈中磁通量Φ随时间t变化的图象.则( )


| A. | 电阻R上的电功率为20 W | |
| B. | 0.02 s时R两端的电压瞬时值为零 | |
| C. | R两端的电压u随时间t变化的规律是u=14.1cos 100πt(V) | |
| D. | 通过R的电流i随时间t变化的规律是i=1.41cos 50πt(A) |
17.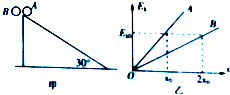 如图所示,A、B两个小球可视为质点,A球沿倾角为30°足够长的光滑斜面由静止开始下滑,B球从与甲球等高处做自由落体运动,A、B两球的动能与位移大小的关系图象如图乙所示.下列说法正确的是( )
如图所示,A、B两个小球可视为质点,A球沿倾角为30°足够长的光滑斜面由静止开始下滑,B球从与甲球等高处做自由落体运动,A、B两球的动能与位移大小的关系图象如图乙所示.下列说法正确的是( )
 如图所示,A、B两个小球可视为质点,A球沿倾角为30°足够长的光滑斜面由静止开始下滑,B球从与甲球等高处做自由落体运动,A、B两球的动能与位移大小的关系图象如图乙所示.下列说法正确的是( )
如图所示,A、B两个小球可视为质点,A球沿倾角为30°足够长的光滑斜面由静止开始下滑,B球从与甲球等高处做自由落体运动,A、B两球的动能与位移大小的关系图象如图乙所示.下列说法正确的是( )| A. | A、B两球的质量之比1:1 | |
| B. | A、B两球的质量之比4:1 | |
| C. | A、B动能为EK0时,重力的瞬时功率之比为1:1 | |
| D. | A、B动能为EK0时,重力的瞬时功率之比为4:1 |
4. 如图所示,一质点做简谐运动,先后以相同的速度依次通过M、N两点,历时1s,质点通过N点后再经过1s又第2次通过N点,在这2s内质点通过的总路程为12cm.则质点的振动周期和振幅分别为( )
如图所示,一质点做简谐运动,先后以相同的速度依次通过M、N两点,历时1s,质点通过N点后再经过1s又第2次通过N点,在这2s内质点通过的总路程为12cm.则质点的振动周期和振幅分别为( )
 如图所示,一质点做简谐运动,先后以相同的速度依次通过M、N两点,历时1s,质点通过N点后再经过1s又第2次通过N点,在这2s内质点通过的总路程为12cm.则质点的振动周期和振幅分别为( )
如图所示,一质点做简谐运动,先后以相同的速度依次通过M、N两点,历时1s,质点通过N点后再经过1s又第2次通过N点,在这2s内质点通过的总路程为12cm.则质点的振动周期和振幅分别为( )| A. | 3 s、6 cm | B. | 4 s、6 cm | C. | 4 s、9 cm | D. | 2 s、8 cm |
1.某质点做简谐运动,其位移随时间变化的关系式为x=10sin($\frac{π}{4}$t)(cm),则下列关于质点运动的说法中正确的是( )
| A. | 质点做简谐运动的振幅为10cm | B. | 质点做简谐运动的周期为4s | ||
| C. | 在t=4s时质点的速度最大 | D. | 在t=4s时质点的位移最大 |

 如图所示方框内有三个电学元件,用多用电表电压挡测量a、b、c、d任意两点间的电压均为零.用欧姆挡测量:
如图所示方框内有三个电学元件,用多用电表电压挡测量a、b、c、d任意两点间的电压均为零.用欧姆挡测量: