题目内容
【题目】如图的环状轨道处于竖直面内，它由半径分别为R和2R的两个半圆轨道、半径为R的两个四分之一圆轨道和两根长度分别为2R和4R的直轨道平滑连接而成．以水平线MN和PQ为界，空间分为三个区域，区域Ⅰ和区域Ⅲ有磁感应强度为B的水平向里的匀强磁场，区域Ⅰ和Ⅱ有竖直向上的匀强电场．一质量为m、电荷量为+q的带电小环穿在轨道内，它与两根直轨道间的动摩擦因数为μ（0＜μ＜1），而轨道的圆弧形部分均光滑．将小环在较长的直轨道CD下端的C点无初速释放（已知区域Ⅰ和Ⅱ的匀强电场场强大小为E= 
，重力加速度为g），
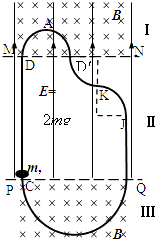
求：
（1）小环在第一次通过轨道最高点A时速度vA的大小；
（2）小环在第一次通过轨道最高点A时受到轨道压力？
（3）若从C点释放小环的同时，在区域Ⅱ再另加一垂直于轨道平面向里的水平匀强电场，其场强大小为E′= 
，则小环在两根直轨道上通过的总路程多大？
【答案】
（1）解：从C到A，洛伦兹力不做功，小环对直轨道无压力，也就不受轨道的摩擦力．由动能定理，有：
qE5R﹣mg5R= 
可得：vA= 
答：小环在第一次通过轨道最高点A时速度vA的大小= ；
（2）解：过A点时，研究小环，由受力分析和牛顿第二定律，有：
FN+mg﹣qvAB﹣qE=m 
解得 FN=11mg+qB 方向向下
答：小环在第一次通过轨道最高点A时受到轨道压力为11mg+qB ，方向向下．
（3）解：由于0＜μ＜1，小环必能通过A点，以后有三种可能：
①有可能第一次过了A点后，恰好停在K点，则在直轨道上通过的总路程为：S总=4R
②也有可能在水平线PQ上方的轨道上往复若干次后，最后一次从A点下来恰好停在K点，对整个运动过程，由动能定理，有：qE3R﹣mg3R﹣μqE′S总=0 得：s总= 
③还可能最终在D或D′点速度为零（即在D与D′点之间振动），由动能定理，有：
qE4R﹣mg4R﹣μqE′S总=0得：s总= 
答：①有可能第一次过了A点后，恰好停在K点，S总=4R；
②也有可能在水平线PQ上方的轨道上往复若干次后，最后一次从A点下来恰好停在K点，s总=
③还可能最终在D或D′点速度为零（即在D与D′点之间振动），s总= ．
【解析】（1）小环从C到A，洛伦兹力不做功，重力做负功，电场力做正功．小环对直轨道无压力，也就不受轨道的摩擦力．根据动能定理求解．
（2）小环在第一次通过轨道最高点A时，受到轨道的弹力，重力，洛伦兹力，电场力，四个力的合力提供向心力，由牛顿第二定律求出轨道的压力．
（3）因为μ＜1，小环在直杆受到的重力与电场力的合力向上，大于滑动摩擦力μmg，则小环必能通过A点．分三种讨论研究：①小环恰好停在K点，②有可能在水平线PQ上方的轨道上往复若干次后，最后一次从A点下来恰好停在K点，③在D与D′点之间振动，小环在D或D′点速度为零．滑动摩擦力做功与路程有关，根据动能定理求解路程．
【考点精析】解答此题的关键在于理解向心力的相关知识，掌握向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力，以及对动能定理的综合应用的理解，了解应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷．
