题目内容
【题目】如图所示，光滑轨道ABCD中BC为四分之一圆孤，圆弧半径为R，CD部分水平，末端D点与右端足够长的水平传送带无缝连接，传送带以恒定的速度v逆时针转动。现将一质量为m的小滑块从轨道上A点由静止释放，A到C的竖直高度为4R，求：
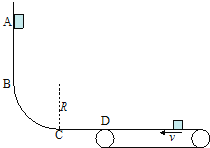
(1)小滑块运动到BC中点时对轨道的压力多大；
(2)若小滑块恰能返回A点，传送带速度的取值范围；
(3)若传送带的速度
，滑块第一次返回D点在传送带上滑动过程中产生的热量为多少。
【答案】（1）
（2）
（3）9mgR
【解析】（1)从A到BC 中点过程中，动能定理得：
在BC中点，根据牛顿第二定律得：
联立以上两式得： 
由牛朝第三定律可细小滑块对轨道的压力大小为.
（2）小滑块从D点滑上传送带先减速为零，然后反向加速，只有当向左滑离D点时的速度与滑上D点的速度相等，小滑块才恰能返回A点，故传送带的速度v≥vD
小滑块由A到D过程中。根据动能定理得：
故
所以传送带的速度
.
(3)设滑块与传送带间的动摩擦因数为μ，小滑块在传送带上滑动时加速度大小a=μg
小滑块从D点滑上传送带到减速为零所用时间为
此过程中产生的热量
小滑块间左加速过程中所需时间为
此过程中产生的热量
所以滑块第一次在传送带上滑动过程中产生的热量Q=9mgR
练习册系列答案
相关题目
