题目内容
9.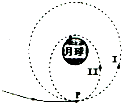 “嫦娥”三号探测器发射到月球上要经过多次变轨,最终降落到月球表面上,其中轨道I为圆形,轨道Ⅱ为椭圆.下列说法正确的是( )
“嫦娥”三号探测器发射到月球上要经过多次变轨,最终降落到月球表面上,其中轨道I为圆形,轨道Ⅱ为椭圆.下列说法正确的是( )| A. | 探测器在轨道Ⅰ的运行周期大于在轨道Ⅱ的运行周期 | |
| B. | 探测器在轨道Ⅰ经过P点时的加速度小于在轨道Ⅱ经过P时的加速度 | |
| C. | 探测器在轨道Ⅰ运行时的加速度大于月球表面的重力加速度 | |
| D. | 探测器在轨道Ⅱ上关闭火箭发动机靠近月球时处于完全失重状态 |
分析 卫星椭圆轨道的半长轴逐渐减小,根据开普勒第三定律,周期要减小;
根据万有引力定律和牛顿第二定律列式判断加速度的大小;
超重和失重只与加速度的方向有关,当加速度为重力加速度且方向向下,物体完全失重.
解答 解:A、轨道I的半长轴比轨道Ⅱ的半长轴大,根据开普勒第三定律,知探测器在轨道I的运行周期大于在轨道Ⅱ的运行周期,故A正确;
B、根据万有引力提供向心力G$\frac{Mm}{{r}^{2}}$=ma,得a=$\frac{GM}{{r}^{2}}$,则知轨道半径相同,则加速度相同,故探测器在轨道I经过P点时的加速度等于在轨道Ⅱ经过P时的加速度,故B错误;
C、探测器在轨道I运行时的万有引力小于在月球表面时的万有引力,根据牛顿第二定律,探测器在轨道I运行时的加速度小于月球表面的重力加速度,故C错误;
D、探测器在轨道Ⅱ上关闭火箭发动机后,只受万有引力,在靠近月球过程中可看成做加速度为重力加速度的加速运动,探测器处于完全失重状态,故D正确.
故选:AD.
点评 本题要掌握万有引力定律和卫星变轨道问题,并要知道卫星绕越运动的向心力由万有引力提供,能结合圆周运动的规律进行求解.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
11.一物体以初速度为v0做匀减速运动,第1s内通过的位移为x1=3m,第2s内通过的位移为x2=2m,物体的速度减小为0时的位移为x,则下列说法中不正确的是( )
| A. | 初速度v0的大小为3.0m/s | B. | 加速度a的大小为1m/s2 | ||
| C. | 位移x的大小为$\frac{49}{8}m$ | D. | 位移x内的平均速度大小为1.75m/s |
20.演示位移传感器的工作原理如图甲所示,物体M在导轨上平移时,带动滑动变阻器的金属杆P,通过理想电压表显示的数据来反映物体的位移x.设电源电动势为E,内阻不计,滑动变阻器的长度为L,物体M以O为平衡位置做简谐运动(取向右为正方向),振幅为$\frac{L}{2}$,物体经过O时P恰好位于滑动变阻器的中点,图乙是电压表的示数U随时间t的变化图象.关于t1时刻物体M的运动情况,下列说法正确的是( )
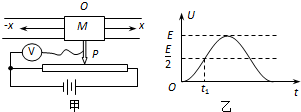

| A. | 物体M具有正方向的最大速度 | |
| B. | 物体M的速度为负方向且正在减小 | |
| C. | 物体M的加速度为零 | |
| D. | 物体M的加速度为负方向且正在增大 |
17. 如图所示为某游乐场的一个娱乐设施,图中的大转盘在竖直平面内匀速转动,坐在吊篮里的游人却显得悠然自得,对某个游人,下列说法正确的是( )
如图所示为某游乐场的一个娱乐设施,图中的大转盘在竖直平面内匀速转动,坐在吊篮里的游人却显得悠然自得,对某个游人,下列说法正确的是( )
 如图所示为某游乐场的一个娱乐设施,图中的大转盘在竖直平面内匀速转动,坐在吊篮里的游人却显得悠然自得,对某个游人,下列说法正确的是( )
如图所示为某游乐场的一个娱乐设施,图中的大转盘在竖直平面内匀速转动,坐在吊篮里的游人却显得悠然自得,对某个游人,下列说法正确的是( )| A. | 他所受合外力恰好为零 | |
| B. | 他所受合外力方向始终指向圆周运动圆心 | |
| C. | 他的机械能保持不变 | |
| D. | 他的机械能不断增加 |
1.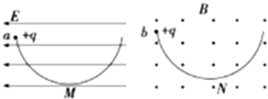 如图所示,两个相同的半圆形光滑绝缘轨道分别竖直放置在匀强电场E和匀强磁场B中,轨道两端在同 一高度上,两个相同的带正电小球a、b同时从轨道左端最高点由静止释放,且在运动过程中始终能通过各自轨道的最低点M、N,则( )
如图所示,两个相同的半圆形光滑绝缘轨道分别竖直放置在匀强电场E和匀强磁场B中,轨道两端在同 一高度上,两个相同的带正电小球a、b同时从轨道左端最高点由静止释放,且在运动过程中始终能通过各自轨道的最低点M、N,则( )
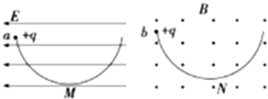 如图所示,两个相同的半圆形光滑绝缘轨道分别竖直放置在匀强电场E和匀强磁场B中,轨道两端在同 一高度上,两个相同的带正电小球a、b同时从轨道左端最高点由静止释放,且在运动过程中始终能通过各自轨道的最低点M、N,则( )
如图所示,两个相同的半圆形光滑绝缘轨道分别竖直放置在匀强电场E和匀强磁场B中,轨道两端在同 一高度上,两个相同的带正电小球a、b同时从轨道左端最高点由静止释放,且在运动过程中始终能通过各自轨道的最低点M、N,则( )| A. | 两小球某次到达轨道最低点时的速度不可能有υN=υM | |
| B. | 两小球都能到达轨道的最右端 | |
| C. | 小球b第一次到达N点的时刻与小球a第一次到达M点的时刻相同 | |
| D. | 小球a受到的电场力一定不大于a的重力,小球b受到的最大洛伦兹力可能大于b的重力 |
18. 如图所示,质量为M木块静止在光滑的水平面上,一颗质量为m的子弹水以速度υ0平射入木块并留在木块中,木块获得的速度为υ1,子弹受到的平均阻力为f,射入深度为d,此过程中木块位移为s,下列说法正确的是( )
如图所示,质量为M木块静止在光滑的水平面上,一颗质量为m的子弹水以速度υ0平射入木块并留在木块中,木块获得的速度为υ1,子弹受到的平均阻力为f,射入深度为d,此过程中木块位移为s,下列说法正确的是( )
 如图所示,质量为M木块静止在光滑的水平面上,一颗质量为m的子弹水以速度υ0平射入木块并留在木块中,木块获得的速度为υ1,子弹受到的平均阻力为f,射入深度为d,此过程中木块位移为s,下列说法正确的是( )
如图所示,质量为M木块静止在光滑的水平面上,一颗质量为m的子弹水以速度υ0平射入木块并留在木块中,木块获得的速度为υ1,子弹受到的平均阻力为f,射入深度为d,此过程中木块位移为s,下列说法正确的是( )| A. | 子弹损失的动能等于fd | |
| B. | 子弹损失的动能为$\frac{1}{2}$mυ02 | |
| C. | 子弹、木块组成的系统损失的动能等于fd | |
| D. | 子弹、木块组成的系统损失的动能为$\frac{1}{2}$(m+M)υ02-$\frac{1}{2}$(m+M)υ12 |
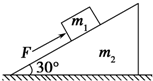 如图所示,质量为m1=5kg的滑块,置于一粗糙的斜面上,用一平行于斜面的大小为30N的力F推滑块,滑块沿斜面向上匀速运动,斜面体质量m2=10kg,且始终静止,取g=10m/s2,求:
如图所示,质量为m1=5kg的滑块,置于一粗糙的斜面上,用一平行于斜面的大小为30N的力F推滑块,滑块沿斜面向上匀速运动,斜面体质量m2=10kg,且始终静止,取g=10m/s2,求: