题目内容
11. 宇宙间存在一些离其它恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量 均为m的星位于等边三角形的三个顶点,三角形边长为L,忽略其它星体对它们的引力作用,三星在同一平面内绕三角形中心O做匀速圆周运动,万有引力常量为G,下列说法正确的是( )
宇宙间存在一些离其它恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量 均为m的星位于等边三角形的三个顶点,三角形边长为L,忽略其它星体对它们的引力作用,三星在同一平面内绕三角形中心O做匀速圆周运动,万有引力常量为G,下列说法正确的是( )| A. | 每颗星做圆周运动的角速度为$\root{3}{\frac{Gm}{{L}^{3}}}$ | |
| B. | 每颗星做圆周运动的加速度与三星的质量无关 | |
| C. | 若距离L和每颗星的质量m都变为原来的2倍,则周期变为原来的2倍 | |
| D. | 若距离L和每颗星的质量m都变为原来的2倍,则线速度变为原来的4倍 |
分析 每颗星做匀速圆周运动,靠另外两颗星万有引力的合力提供向心力,具有相同的角速度,根据合力提供向心力求出角速度的大小、向心加速度的大小,以及周期和线速度的大小,从而分析判断.
解答 解:任意两个星星之间的万有引力为:F=$G\frac{{m}^{2}}{{L}^{2}}$,
则其中一颗星星所受的合力${F}_{合}=2Fcos30°=\sqrt{3}F=\frac{\sqrt{3}G{m}^{2}}{{L}^{2}}$,
根据$\frac{\sqrt{3}G{m}^{2}}{{L}^{2}}=ma=m\frac{{v}^{2}}{r}=mr{ω}^{2}=mr\frac{4{π}^{2}}{{T}^{2}}$得,
r=$\frac{\sqrt{3}}{3}L$,
解得ω=$\sqrt{\frac{3Gm}{{L}^{3}}}$,故A错误.
加速度a=$\frac{\sqrt{3}Gm}{{L}^{2}}$,与三星的质量有关,故B错误.
周期T=$2π\sqrt{\frac{{L}^{3}}{3Gm}}$,若距离L和每颗星的质量m都变为原来的2倍,则周期变为原来的2倍,故C正确.
线速度v=$\sqrt{\frac{Gm}{L}}$,若距离L和每颗星的质量m都变为原来的2倍,则线速度大小不变,故D错误.
故选:C.
点评 解决该题首先要理解模型所提供的情景,然后能够列出合力提供向心力的公式,才能正确解答题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.某质点做简谐运动,其位移随时间变化的关系式为x=10sin($\frac{π}{4}$t)(cm),则下列关于质点运动的说法中正确的是( )
| A. | 质点做简谐运动的振幅为10cm | B. | 质点做简谐运动的周期为4s | ||
| C. | 在t=4s时质点的速度最大 | D. | 在t=4s时质点的位移最大 |
6.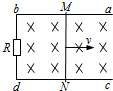 如图所示,两根相距为l的平行直导轨ab、cd,b、d间连有一固定电阻R,导轨电阻可忽略不计.MN为放在ab和cd上的一导体杆,与ab垂直,其电阻也为R.整个装置处于匀强磁场中,磁感应强度的大小为B,磁场方向垂直于导轨所在平面(垂直纸面向里).现对MN施力使它沿导轨方向以速度v水平向右做匀速运动.令U表示MN两端电压的大小,则( )
如图所示,两根相距为l的平行直导轨ab、cd,b、d间连有一固定电阻R,导轨电阻可忽略不计.MN为放在ab和cd上的一导体杆,与ab垂直,其电阻也为R.整个装置处于匀强磁场中,磁感应强度的大小为B,磁场方向垂直于导轨所在平面(垂直纸面向里).现对MN施力使它沿导轨方向以速度v水平向右做匀速运动.令U表示MN两端电压的大小,则( )
 如图所示,两根相距为l的平行直导轨ab、cd,b、d间连有一固定电阻R,导轨电阻可忽略不计.MN为放在ab和cd上的一导体杆,与ab垂直,其电阻也为R.整个装置处于匀强磁场中,磁感应强度的大小为B,磁场方向垂直于导轨所在平面(垂直纸面向里).现对MN施力使它沿导轨方向以速度v水平向右做匀速运动.令U表示MN两端电压的大小,则( )
如图所示,两根相距为l的平行直导轨ab、cd,b、d间连有一固定电阻R,导轨电阻可忽略不计.MN为放在ab和cd上的一导体杆,与ab垂直,其电阻也为R.整个装置处于匀强磁场中,磁感应强度的大小为B,磁场方向垂直于导轨所在平面(垂直纸面向里).现对MN施力使它沿导轨方向以速度v水平向右做匀速运动.令U表示MN两端电压的大小,则( )| A. | U=$\frac{1}{2}$Blv,流过固定电阻R的感应电流由b经R到d | |
| B. | U=Blv,流过固定电阻R的感应电流由d经R到b | |
| C. | MN受到的安培力大小FA=$\frac{{B}^{2}{l}^{2}v}{2R}$,方向水平向右 | |
| D. | MN受到的安培力大小FA=$\frac{{B}^{2}{l}^{2}v}{R}$,方向水平向左 |
16.如图甲所示为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x=1m处的质点,Q是平衡位置为x=4m处的质点,如图乙所示为质点Q的振动图象,下列说法正确的是( )

| A. | t=0.15s时,质点Q的加速度达到正向最大 | |
| B. | t=0.15s时,质点P的运动方向沿y轴负方向 | |
| C. | t=0.25s时,质点P的动能在减少 | |
| D. | 从t=0.10s到t=0.25s,该波沿轴轴负方向传播了6m | |
| E. | 从t=0.10s到t=0.25s,质点p通过的路程为15cm |
20.若以V表示在标准状态下水蒸气的摩尔体积,ρ表示在标准状态下水蒸气的密度,M表示水的摩尔质量,M0表示一个水分子的质量,V0表示一个水分子的体积,NA表示阿伏加德罗常数,则下列关系式中正确的是( )
| A. | V=$\frac{M}{ρ}$ | B. | V0=$\frac{V}{{N}_{A}}$ | C. | M0=$\frac{M}{{N}_{A}}$ | D. | ρ=$\frac{M}{{N}_{A}{V}_{0}}$ | ||||
| E. | NA=$\frac{ρV}{{M}_{0}}$ |
1. 如图所示,xOy平面是无穷大导体的表面,该导体充满z<0的空间,z>0的空间为真空.将电量为q的点电荷置于z轴上z=h处,则在平面xOy上会产生感应电荷.空间任意一点处的电场皆是由点电荷和导体表面上的感应电荷共同激发的.已知静电平衡时导体内部场强处处为零,则在z轴上z=$\frac{h}{2}$处的场强大小为(k为静电力常量)( )
如图所示,xOy平面是无穷大导体的表面,该导体充满z<0的空间,z>0的空间为真空.将电量为q的点电荷置于z轴上z=h处,则在平面xOy上会产生感应电荷.空间任意一点处的电场皆是由点电荷和导体表面上的感应电荷共同激发的.已知静电平衡时导体内部场强处处为零,则在z轴上z=$\frac{h}{2}$处的场强大小为(k为静电力常量)( )
 如图所示,xOy平面是无穷大导体的表面,该导体充满z<0的空间,z>0的空间为真空.将电量为q的点电荷置于z轴上z=h处,则在平面xOy上会产生感应电荷.空间任意一点处的电场皆是由点电荷和导体表面上的感应电荷共同激发的.已知静电平衡时导体内部场强处处为零,则在z轴上z=$\frac{h}{2}$处的场强大小为(k为静电力常量)( )
如图所示,xOy平面是无穷大导体的表面,该导体充满z<0的空间,z>0的空间为真空.将电量为q的点电荷置于z轴上z=h处,则在平面xOy上会产生感应电荷.空间任意一点处的电场皆是由点电荷和导体表面上的感应电荷共同激发的.已知静电平衡时导体内部场强处处为零,则在z轴上z=$\frac{h}{2}$处的场强大小为(k为静电力常量)( )| A. | k$\frac{4q}{{r}^{2}}$ | B. | k$\frac{4q}{9{r}^{2}}$ | C. | k$\frac{32q}{9{r}^{2}}$ | D. | k$\frac{40q}{9{r}^{2}}$ |

 、电阻箱R、定值电阻( R0=5Ω)、开关S、若干导线和该电池连成电路,进一步测定该电池电动势和内阻.
、电阻箱R、定值电阻( R0=5Ω)、开关S、若干导线和该电池连成电路,进一步测定该电池电动势和内阻. 相应示数U.记录多组R、U数据,并计算出相应的$\frac{1}{R}$与$\frac{1}{U}$的值,做出$\frac{1}{R}$-$\frac{1}{U}$图线如图c所示.分析该图线斜率k 的物理意义知k=$\frac{{R}_{0}+r}{E}$.(用E、r、R0表示)
相应示数U.记录多组R、U数据,并计算出相应的$\frac{1}{R}$与$\frac{1}{U}$的值,做出$\frac{1}{R}$-$\frac{1}{U}$图线如图c所示.分析该图线斜率k 的物理意义知k=$\frac{{R}_{0}+r}{E}$.(用E、r、R0表示) 冰壶在水平而上某次滑行可简化为如下过程:如图所示,运动员给冰壶施加一水平恒力将静止于A点的冰壶(视为质点)沿直线AD推到B点放手,最后冰壶停于D点.已知冰壶与冰面间的动摩擦因数为μ,AB=CD=l、BC=7l,重力加速度为g.求:
冰壶在水平而上某次滑行可简化为如下过程:如图所示,运动员给冰壶施加一水平恒力将静止于A点的冰壶(视为质点)沿直线AD推到B点放手,最后冰壶停于D点.已知冰壶与冰面间的动摩擦因数为μ,AB=CD=l、BC=7l,重力加速度为g.求: