题目内容
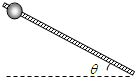
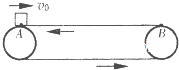
如图所示的传送带，其水平部分ab=2.09m，倾斜部分bc=3.2m，与水平夹角为37°，皮带沿图示方向运动，速率恒为2m/s，把物体A轻放在点c处，它将被皮带送到a点，且物体A一直没脱离皮带．若物体A与传送带间的动摩擦因数μ=0.8，求物体A从c点被传送到a点所用的时间．（g取10m/s2，sin37°=0.6，cos37°=0.8）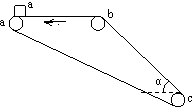
物体由c到b过程，根据牛顿第二定律得，μmgcosθ-mgsinθ=ma
解得a=0.4m/s2
根据v=at得，2=0.4t
解得t=5s
x=
at2＞3.2m
则3.2=
at12，解得t1=4s
v=at1=1.6m/s
在b到a的过程中，先做匀加速直线运动，达到传送带速度后做匀速直线运动．
加速度a′=μg=8m/s2．
物体由b到a的过程，有v=1.6+8t2，解得t2=0.05s
x2=vt2+
a′t22=1.6t2+4t22=0.09m
则匀速运动的位移为2.09-0.09m=2m
t3=
=1s
所以全程时间t=t1+t2+t3=5.05s．
答：物体A从c点被传送到a点所用的时间为5.05s．
解得a=0.4m/s2
根据v=at得，2=0.4t
解得t=5s
x=
| 1 |
| 2 |
则3.2=
| 1 |
| 2 |
v=at1=1.6m/s
在b到a的过程中，先做匀加速直线运动，达到传送带速度后做匀速直线运动．
加速度a′=μg=8m/s2．
物体由b到a的过程，有v=1.6+8t2，解得t2=0.05s
x2=vt2+
| 1 |
| 2 |
则匀速运动的位移为2.09-0.09m=2m
t3=
| 2 |
| v |
所以全程时间t=t1+t2+t3=5.05s．
答：物体A从c点被传送到a点所用的时间为5.05s．
练习册系列答案
阅读快车系列答案
相关题目
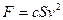，式中S为鸟翅膀的面积，v为鸟飞行的速度，c是恒量，鸟类能飞起的条件是
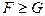，即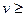
_________，取等号时的速率为临界速率。
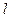，质量
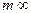体积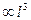
，
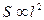，于是起飞的临界速率
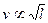。燕子的滑翔速率最小大约为20 km/h，而鸵鸟的体长大约是燕子的25倍，从而跑动起飞的临界速率为________km/h，而实际上鸵鸟的奔跑速度大约只有40km/h，可见，鸵鸟是飞不起来的，我们在生活中还可以看到，像麻雀这样的小鸟，只需从枝头跳到空中，用翅膀拍打一两下，就可以飞起来。而像天鹅这样大的飞禽，则首先要沿着地面或水面奔跑一段才能起飞，这是因为小鸟的_______，而天鹅的______。
