题目内容
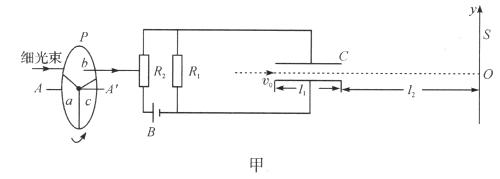
【题目】图甲中B为电源,电动势![]() ,内阻不计.固定电阻
,内阻不计.固定电阻![]() ,
,![]() 为光敏电阻.C为平行板电容器,虚线到两极板距离相等,极板长
为光敏电阻.C为平行板电容器,虚线到两极板距离相等,极板长![]() ,两极板的间距
,两极板的间距![]() .S为屏,与极板垂直,到极板的距离
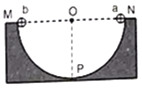
.S为屏,与极板垂直,到极板的距离![]() .P为一圆盘,由形状相同、透光率不同的三个扇形a、b和c构成,它可绕
.P为一圆盘,由形状相同、透光率不同的三个扇形a、b和c构成,它可绕![]() 轴转动.当细光束通过扇形a、b、c照射光敏电阻
轴转动.当细光束通过扇形a、b、c照射光敏电阻![]() 时,
时,![]() 的阻值分别为
的阻值分别为![]() 、
、![]() 、
、![]() .有一细电子束沿图中虚线以速度
.有一细电子束沿图中虚线以速度![]() 连续不断地射入C.已知电子电量
连续不断地射入C.已知电子电量![]() ,电子质量
,电子质量![]() .忽略细光束的宽度、电容器的充电放电时间及电子所受的重力.假设照在
.忽略细光束的宽度、电容器的充电放电时间及电子所受的重力.假设照在![]() 上的光强发生变化时
上的光强发生变化时![]() 阻值立即有相应的改变.
阻值立即有相应的改变.
(1)设圆盘不转动,细光束通过b照射到![]() 上,求电子到达屏S上时,它离O点的距离
上,求电子到达屏S上时,它离O点的距离![]() (计算结果保留
(计算结果保留
两位有效数字).
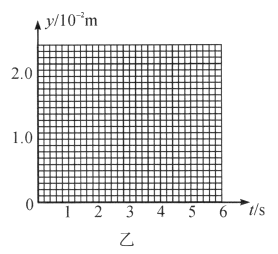
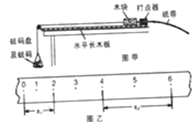
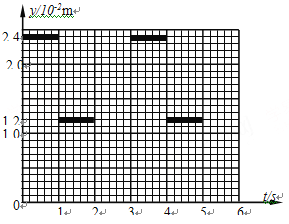
(2)设转盘按图甲中箭头方向匀速转动,每3s转一圈.取光束照在a、b分界处时![]() ,试在图乙给出的坐标纸上,画出电子到达屏S上时,它离O点的距离y随时间t的变化图线(0~6s).要求在y轴上标出图线上最高点与最低点的值(不要求写出计算过程).
,试在图乙给出的坐标纸上,画出电子到达屏S上时,它离O点的距离y随时间t的变化图线(0~6s).要求在y轴上标出图线上最高点与最低点的值(不要求写出计算过程).
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
试题(1)设电容器C两板间的电压为U,电场强度大小为E,电子在极板间穿行时y方向上的加速度大小为a,穿过C的时间为t1,穿出时电子偏转的距离为y1,
![]()
![]()
![]()
![]()
![]()
由以上各式得![]() 代入数据可得
代入数据可得![]()
由此可见![]() ,电子可通过C。
,电子可通过C。
设电子从C穿出时,沿y方向的速度为![]() ,穿出后到达屏S所经历的时间为
,穿出后到达屏S所经历的时间为![]() ,在此时间内电子在y方向移动的距离为
,在此时间内电子在y方向移动的距离为![]() ,
,
![]()
![]()
![]()
由以上关系式得![]()
代入数据得![]()
由题意得![]()
(2)如图所示。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目