题目内容
【题目】质量为m的甲物块以3 m/s的速度在光滑水平面上运动,有一轻弹簧固定在甲物块上。另一质量也为m的乙物块以4 m/s的速度与甲相向运动,如图所示。则( )

A. 甲、乙两物块在压缩弹簧过程中,由于弹力作用,系统动量不守恒
B. 当两物块相距最近时,甲物块的速率为零
C. 当甲物块的速率为1m/s时,乙物块的速率可能为2 m/s,也可能为0
D. 甲物块的速率可能达到5 m/s
【答案】C
【解析】甲、乙两物块(包括弹簧)组成的系统在弹簧压缩过程中,系统所受的合外力为零,系统动量守恒,故A错误;当两物块相距最近时速度相同,取碰撞前乙的速度方向为正方向,设共同速率为v,由动量守恒定律得:mv乙-mv甲=2mv,代入数据解得:v=0.5m/s,故B错误.甲、乙组成的系统动量守恒,若物块甲的速率为1m/s,方向与原来相同,由动量守恒定律得:mv乙-mv甲=-mv甲′+m乙v乙′,代入数据解得:v乙′=2m/s;若物块甲的速率为1m/s,方向与原来相反,由动量守恒定律得:mv乙-mv甲=mv甲′+m乙v乙′,代入数据解得:v乙′=0,故C正确.若物块甲的速率达到5m/s,方向与原来相同,则:mv乙-mv甲=-mv甲′+m乙v乙′,代入数据代入解得:v乙′=6m/s.两个物体的速率都增大,动能都增大,违反了能量守恒定律.若物块甲的速率达到5m/s,方向与原来相反,则:mv乙-mv甲=mv甲′+m乙v乙′,代入数据解得:v乙′=-4m/s,可以,碰撞后,乙的动能不变,甲的动能增加,系统总动能增加,违反了能量守恒定律.所以物块甲的速率不可能达到5m/s,故D错误.故选C.

【题目】某同学利用下述装置对轻质弹簧的弹性势能进行探究,一轻质弹簧放置在光滑水平桌面上,弹簧左端固定,右端与一小球接触而不固连:弹簧处于原长时,小球恰好在桌面边缘,如图(a)所示.向左推小球,使弹黄压缩一段距离后由静止释放:小球离开桌面后落到水平地面.通过测量和计算,可求得弹簧被压缩后的弹性势能.回答下列问题:
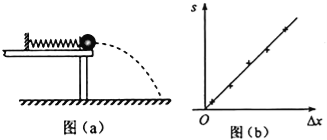
(1)本实验中可认为,弹簧被压缩后的弹性势能Ep与小球抛出时的动能Ek相等.已知重力加速度大小为g.为求得Ek,至少需要测量下列物理量中的 (填正确答案标号).
A.小球的质量m |
B.小球抛出点到落地点的水平距离s |
C.桌面到地面的高度h |
D.弹簧的压缩量△x |
E.弹簧原长l0
(2)用所选取的测量量和已知量表示Ek,得Ek= .
(3)图(b)中的直线是实验测量得到的s﹣△x图线.从理论上可推出,如果h不变.m增加,s﹣△x图线的斜率会 (填“增大”、“减小”或“不变”):如果m不变,h增加,s﹣△x图线的斜率会 (填“增大”、“减小”或“不变”).由图(b) 中给出的直线关系和Ek的表达式可知,Ep与△x的 次方成正比.