Question

【题目】用一根长为l的轻质不可伸长的细绳把一个质量为m的小球悬挂在点O，将小球拉至与悬点等高处由静止释放，如图所示．求：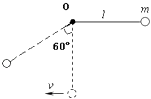

（1）小球经过最低点时，速度大小及细绳的拉力大小．
（2）小球经过最低点左边与竖直方向成60°角位置时，速度大小．

Answer 1

【答案】
（1）解：从静止运动到最低点的过得中，机械能守恒，则有：

mgl= mv2

则得小球经过最低点时的速度大小为：v=

在最低点，根据牛顿第二定律得：

F﹣mg=m

联立上两式得：F=3mg

答：小球经过最低点时，速度大小为 ，细绳的拉力大小为3mg．

（2）从开始到小球左边与竖直方向成60°角位置的过程中，根据机械能守恒定律得：

mglcos60°=

解得：v′=

答：小球经过最低点左边与竖直方向成60°角位置时，速度大小为 ．

【解析】（1）小球拉至与悬点等高处由静止释放，从静止运动到最低点的过得中，机械能守恒，可以求出小球经过最低点时的速度，结合向心力公式可以求出细绳的拉力大小。
（2）从开始到小球左边与竖直方向成60°角位置的过程中，小球机械能守恒，减少的重力势能全部转化为动能，列式可以求出小球经过最低点左边与竖直方向成60°角位置时速度的大小。
【考点精析】利用向心力和机械能守恒及其条件对题目进行判断即可得到答案，需要熟知向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力；在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变．