题目内容
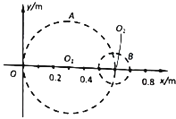
【题目】在xOy平面内分布着垂直纸面向里的匀强磁场，磁感应强度B＝0.01T，其中有一半径为R＝0.lm的无磁场圆形区域，圆心在原点O（0，0），如图所示。位于直线：x＝一0.3m上的粒子源可以沿直线移动，且沿x轴正向发射质量m＝1.0×10－14kg、电荷量q＝一1.0×10－6C、速率v＝4.0×105m/s的粒子，忽略粒子间的相互作用，不计粒子的重力。
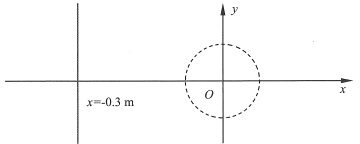
（1）求从粒子源发射的粒子运动到圆形区域所用的最短时间。
（2）在直线x＝－0.3m上什么范围内发射的粒子才能进人圆形区域？
（3）若在直线x＝－0.3m处放置一足够长的荧光屏，将上述粒子源放在原点O，仅改变发射粒子的速度方向，求粒子能打中荧光屏最高点的纵坐标ym。
【答案】（1）
（2）0≤y≤0.8m （3）0.4m
【解析】（1）设粒子在磁场中匀速圆周运动的半径为r，
由牛顿第二定律
，解得
如图1所示，经过（－0.1m，0）的粒子进入圆形区域的时间最短，由几何关系得
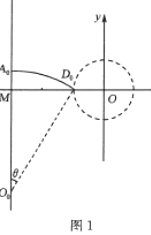
由圆周运动公式
，
，联立解得：
（或0.52×10－６s）
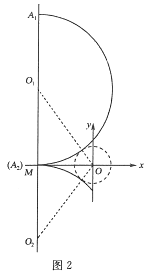
（2）如图2所示，在A1点发射的粒子恰好能进人圆形区域。由几何关系
，
，解得
如图2所示，在A2点发射的粒子恰好能进入圆形区域，由几何关系
，
解得：
（即A2与M重合)
综上，在直线x=－0.3m上，0≤y≤0.8m范围内发射的粒子才能进入圆形区域。
（3）粒子从原点O（0，0）发射，初速度方向与x轴负方向成角，轨迹与荧光屏相切与D点（一0.3，y）。由几何关系
解得
而
，解得：
练习册系列答案
相关题目
