Question

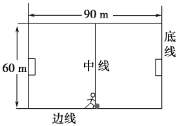
【题目】有一种公交电车站，车站站台的路轨建得高些，车辆进站时要上坡，出站时要下坡，如图甲所示，这样既可以节能又可以节省停车所需的时间。为简化问题，现设两边倾斜部分AB 段和CD 段均为直轨道，长度均为L=200 m，水平部分BC 段长度也为L=200 m、站台的高度 h 未知，如图乙所示，各段道路交接处均为圆滑连接。一长度可忽略的电车自站台左前方以 v0=72 km/h 的速度驶向站台，为了节能，司机在未到站时即关闭电车电源，经过时间 t1=100 s 后到达 A 点，接着冲上了倾斜轨道，到达站台上的 B 点时速度为 vB=18 km/h，此时司机还需启动刹车系统，使得电车最终正好停在了 BC 段的中点。已知电车在各段轨道上所受摩擦（不含刹车时所增加的阻力）及空气阻力均可认为等于其自身总重量的 0.01 倍，刹车过程所增加的阻力可看作恒力，忽略电车经过各道路交接处的能量损失及可能腾空对研究问题的影响，g 取 10 m/s2 求：

（1）电车到达 A 点时的速度大小 vA；

（2）电车从站台 B 点到最终停止所需的时间 t；

（3）该电车站台的高度 h；

Answer 1

【答案】（1）10m/s；（2）40s；（3）1.75m。

【解析】

v0=72km/h=20m/s，vB=18km/h=5m/s；
（1）电车从切断电源到A点的过程合外力为摩擦力，故由牛顿第二定律可得：0.01mg=ma1，所以，a1＝0.01g＝0.1m/s2；

由匀变速运动规律可得：vA=v0-a1t1=20m/s-0.1×100m/s=10m/s；
（2）机车从B点到停止的过程受重力、支持力、摩擦力和阻力作用，故机车做匀减速运动，则有L＝vBt，所以，电车从站台B点到最终停止所需的时间；
（3）机车从A点到B点的过程只有重力和摩擦力做功，故由动能定理可得：mgh0.01mgL＝mvB2mvA2；
所以，