题目内容
4. 质量为M的光滑圆槽放在光滑水平面上,一水平恒力F作用在其上促使质量为m的小球静止在圆槽上,如图所示,则( )
质量为M的光滑圆槽放在光滑水平面上,一水平恒力F作用在其上促使质量为m的小球静止在圆槽上,如图所示,则( )| A. | 小球对圆槽的压力为$\sqrt{(m{g}^{2})+(\frac{mF}{M+m})^{2}}$ | |
| B. | 小球对圆槽的压力为$\frac{mF}{M+m}$ | |
| C. | 水平恒力F变大后,如果小球仍静止在圆槽上,小球对圆槽的压力不变 | |
| D. | 水平恒力F变大后,如果小球仍静止在圆槽上,小球对圆槽的压力减小 |
分析 对整体分析,根据牛顿第二定律求出整体的加速度,隔离对小球分析,求出小球受到圆槽的支持力,结合表达式判断压力与水平恒力F的关系.
解答 解:A、利用整体法可求得系统的加速度为:a=$\frac{F}{M+m}$,对小球利用牛顿第二定律可得小球受到圆槽的支持力为:$N=\sqrt{(ma)^{2}+(mg)^{2}}$=$\sqrt{(mg)^{2}+\frac{{m}^{2}{F}^{2}}{(M+m)^{2}}}$,
由牛顿第三定律可知小球对圆槽的压力为N′=$\sqrt{(mg)^{2}+\frac{{m}^{2}{F}^{2}}{(M+m)^{2}}}$.故A正确,B错误.
C、由压力的表达式知,F增大后,如果小球仍静止在圆槽上,小球对圆槽的压力增加,故C错误,D错误.
故选:A.
点评 本题考查了牛顿第二定律的基本运用,知道圆槽和小球具有相同的加速度,运用整体法和隔离法进行求解,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下表是在北京西与长沙区间运行的T1/T2次列车运行时刻表.假设列车准点到达和准点开出,且做直线运动.求:
(1)列车由长沙开出到达武昌的过程中的平均速度;
(2)列车由郑州开出到达岳阳的过程中的平均速度;
(3)T1次列车在5:05时的速度和全程的平均速度.(结果单位均以km/h表示)
| 北京西 ↓ 长沙 (T1次) | 自北京西起 里程(km) | 站名 | 北京西 ↑ 长沙 (T2次) |
| 17:00 | 0 | 北京西 | 8:14 |
| 23:29 23:35 | 690 | 郑州 | 1:40 1:39 |
| 5:01 5:09 | 1226 | 武昌 | 20:12 20:04 |
| 7:12 7:18 | 1441 | 岳阳 | 17:58 17:56 |
| 8:38 | 1588 | 长沙 | 16:36 |
(2)列车由郑州开出到达岳阳的过程中的平均速度;
(3)T1次列车在5:05时的速度和全程的平均速度.(结果单位均以km/h表示)
15. 如图所示,A、B两质点以相同的水平速度v0抛出,A在竖直面内运动,落地点P1,B沿光滑斜面运动,落地点为P2,不计空气阻力,比较P1、P2 在x轴方向上距抛出点的远近关系及落地瞬时速度的大小关系,则有( )
如图所示,A、B两质点以相同的水平速度v0抛出,A在竖直面内运动,落地点P1,B沿光滑斜面运动,落地点为P2,不计空气阻力,比较P1、P2 在x轴方向上距抛出点的远近关系及落地瞬时速度的大小关系,则有( )
 如图所示,A、B两质点以相同的水平速度v0抛出,A在竖直面内运动,落地点P1,B沿光滑斜面运动,落地点为P2,不计空气阻力,比较P1、P2 在x轴方向上距抛出点的远近关系及落地瞬时速度的大小关系,则有( )
如图所示,A、B两质点以相同的水平速度v0抛出,A在竖直面内运动,落地点P1,B沿光滑斜面运动,落地点为P2,不计空气阻力,比较P1、P2 在x轴方向上距抛出点的远近关系及落地瞬时速度的大小关系,则有( )| A. | P1较近 | B. | P1、P2一样远 | ||
| C. | A落地时,速率大 | D. | A、B落地时,速率一样大 |
12.骑自行车的人沿着直线从静止开始运动,运动后,在第1s、第2s、第3s、第4s内,通过的路程分别为1m、2m、3m、4m,有关其运动的描述正确的是( )
| A. | 前4 s内的平均速度是2.5 m/s | B. | 在第3、4 s内平均速度是3.5 m/s | ||
| C. | 第3 s末的瞬时速度一定是3 m/s | D. | 第2s内的平均速度是1m/s |
9.2012年11月,“歼15”舰载机在“辽宁号”航空母舰上着舰成功.图(a)为利用阻拦系统让舰载机在飞行甲板上快速停止的原理示意图.飞机着舰并成功钩住阻拦索后,飞机的动力系统立即关闭,阻拦系统通过阻拦索对飞机施加一作用力,使飞机在甲板上短距离滑行后停止.某次降落,以飞机着舰为计时零点,飞机在t=0.4s时恰好钩住阻拦索中间位置,其着舰到停止的速度一时间图线如图(b)所示.假如无阻拦索,飞机从着舰到停止需要的滑行距离约为1 000m.已知航母始终静止,重力加速度的大小为g.则( )

| A. | 在0.4 s~2.5 s时问内,阻拦索的张力几乎不随时间变化 | |
| B. | 从着舰到停止,飞机在甲板上滑行的距离约为无阻拦索时的$\frac{1}{10}$ | |
| C. | 在滑行过程中,飞行员所承受的加速度大小不会超过2.5g | |
| D. | 在0.4 s~2.5 s时间内,阻拦系统对飞机做功的功率逐渐减小 |
16.传感器是把非电学物理量(如位移、速度、压力、角度等)转换成电学物理量(如电压、电流、电量等)的一种元件.如图所示中的甲、乙、丙、丁是四种常见的电容式传感器,已知电容器两极间的电压始终不变,则下列说法正确的是( )


| A. | 若电量增加,可判断出θ变大 | B. | 若电量减少,可判断出h变小 | ||
| C. | 若有电流向传感器充电,则F变大 | D. | 若有电流沿传感器放电,则x变大 |
13.有一条两岸平行、河水均匀流动、流速恒为v的大河,小明驾着小船渡河,去程时船头朝向始终与河岸垂直,回程时行驶路线与河岸垂直.去程与回程所走的位移的比值为k,船在静水中的速度大小相同,则小船去程与回程所用时间的比值为( )
| A. | $\frac{k}{\sqrt{{k}^{2}-1}}$ | B. | $\frac{1}{\sqrt{{k}^{2}-1}}$ | C. | $\frac{1}{\sqrt{{k}^{2}-2}}$ | D. | $\sqrt{2-{k}^{2}}$ |
7. 如图所示内壁光滑,质量为m的箱子A放在倾角为θ的光滑斜面上,为了防止箱子下滑用轻绳固定在斜面上的D柱,箱子中有质量均为m的小球B和C通过轻弹簧相连,然后C通过细绳固定在箱子上,求烧断箱子和D柱之间细线的瞬间,A、B的加速度分别为( )
如图所示内壁光滑,质量为m的箱子A放在倾角为θ的光滑斜面上,为了防止箱子下滑用轻绳固定在斜面上的D柱,箱子中有质量均为m的小球B和C通过轻弹簧相连,然后C通过细绳固定在箱子上,求烧断箱子和D柱之间细线的瞬间,A、B的加速度分别为( )
 如图所示内壁光滑,质量为m的箱子A放在倾角为θ的光滑斜面上,为了防止箱子下滑用轻绳固定在斜面上的D柱,箱子中有质量均为m的小球B和C通过轻弹簧相连,然后C通过细绳固定在箱子上,求烧断箱子和D柱之间细线的瞬间,A、B的加速度分别为( )
如图所示内壁光滑,质量为m的箱子A放在倾角为θ的光滑斜面上,为了防止箱子下滑用轻绳固定在斜面上的D柱,箱子中有质量均为m的小球B和C通过轻弹簧相连,然后C通过细绳固定在箱子上,求烧断箱子和D柱之间细线的瞬间,A、B的加速度分别为( )| A. | 0 0 | B. | 3gsinθ 0 | ||
| C. | $\frac{3}{2}$gsinθ 0 | D. | gsinθ gsinθ |
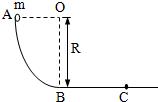 AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示.一小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.(重力加速度为g)求:
AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示.一小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.(重力加速度为g)求: