题目内容
19.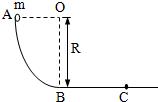 AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示.一小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.(重力加速度为g)求:
AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示.一小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.(重力加速度为g)求:(1)小球运动到B点时的动能
(2)小球下滑到距水平轨道的高度为h=$\frac{R}{3}$时的速度大小
(3)小球经过圆弧轨道的B点和水平轨道的C点时,所受轨道支持力NB、NC各是多大?
分析 (1)根据动能定理求出小球运动到B点的动能.
(2)根据动能定理求出小球下滑到距水平轨道的高度为h=$\frac{R}{3}$时的速度大小.
(3)根据动能定理求出B点的速度,结合牛顿第二定律求出支持力的大小,在C点,根据平衡求出支持力的大小.
解答 解:(1)根据动能定理得:mgR=$\frac{1}{2}m{{v}_{B}}^{2}$,
解得:EkB=mgR.
(2)根据动能定理得:$mg(R-h)=\frac{1}{2}m{v}^{2}$,
解得:v=$\sqrt{\frac{4gR}{3}}$.
(3)根据mgR=$\frac{1}{2}m{{v}_{B}}^{2}$得:${v}_{B}=\sqrt{2gR}$,
根据牛顿第二定律得:${N}_{B}-mg=m\frac{{{v}_{B}}^{2}}{R}$,
解得:NB=3mg.
运动到C点时,有:NC=mg.
答:(1)小球运动到B点的动能为mgR.
(2)小球下滑到距水平轨道的高度为h=$\frac{R}{3}$时的速度大小为$\sqrt{\frac{4gR}{3}}$.
(3)所受轨道支持力NB、NC各是3mg、mg.
点评 本题考查了动能定理和牛顿第二定律的基本运用,知道圆弧最低点向心力的来源,结合动能定理和牛顿第二定律综合求解.

练习册系列答案
相关题目
9.为了测定一节干电池的电动势和内电阻,现准备了下列器材:
A.待测干电池E(电动势约1.5V,内阻约1.0Ω);
B.电流表G(满偏电流3.0mA,内阻10Ω);
C.电流表A(量程0~0.60A,内阻0.10Ω);
D.滑动变阻器R1(阻值范围为0~20Ω,额定电流为2A);
E.滑动变阻器R2(阻值范围为0~1000Ω,额定电流为1A);
F.定值电阻R3=990Ω;
G.开关K和导线若干.

(1)为了能尽量准确地进行测量,也为了操作方便,实验中应选用的滑动变阻器是R1(填仪器代号).
(2)请在图甲方框中画出实验电路原理图,并注明器材的字母代号.
(3)请根据你在图甲方框中所画的实验电路原理图,在图乙所示的实物图中用笔画线代替导线,完成实验电路.
(4)表为某同学根据正确的电路图所测得的实验数据(I1为电流表G的示数,I2为电流表A的示数).
请在图丙的坐标系中标出适当的坐标值并作出I1-I2的图象.
(5)根据你所画出的I1-I2图象,可求得被测干电池的电动势E=1.45V,内电阻r=0.90Ω.(小数点后面保留两位数字)
A.待测干电池E(电动势约1.5V,内阻约1.0Ω);
B.电流表G(满偏电流3.0mA,内阻10Ω);
C.电流表A(量程0~0.60A,内阻0.10Ω);
D.滑动变阻器R1(阻值范围为0~20Ω,额定电流为2A);
E.滑动变阻器R2(阻值范围为0~1000Ω,额定电流为1A);
F.定值电阻R3=990Ω;
G.开关K和导线若干.

(1)为了能尽量准确地进行测量,也为了操作方便,实验中应选用的滑动变阻器是R1(填仪器代号).
(2)请在图甲方框中画出实验电路原理图,并注明器材的字母代号.
(3)请根据你在图甲方框中所画的实验电路原理图,在图乙所示的实物图中用笔画线代替导线,完成实验电路.
(4)表为某同学根据正确的电路图所测得的实验数据(I1为电流表G的示数,I2为电流表A的示数).
| I2/A | 0.10 | 0.20 | 0.28 | 0.40 |
| I1/mA | 1.39 | 1.32 | 1.25 | 1.16 |
(5)根据你所画出的I1-I2图象,可求得被测干电池的电动势E=1.45V,内电阻r=0.90Ω.(小数点后面保留两位数字)
7. 如图所示,自动卸货车始终静止在水平地面上,车厢在液压机的作用下可以改变与水平面间的倾角θ,用以卸下车厢中的货物.下列说法正确的是( )
如图所示,自动卸货车始终静止在水平地面上,车厢在液压机的作用下可以改变与水平面间的倾角θ,用以卸下车厢中的货物.下列说法正确的是( )
 如图所示,自动卸货车始终静止在水平地面上,车厢在液压机的作用下可以改变与水平面间的倾角θ,用以卸下车厢中的货物.下列说法正确的是( )
如图所示,自动卸货车始终静止在水平地面上,车厢在液压机的作用下可以改变与水平面间的倾角θ,用以卸下车厢中的货物.下列说法正确的是( )| A. | 当货物相对车厢静止时,随着θ角的增大货物与车厢间的摩擦力增大 | |
| B. | 当货物相对车厢静止时,随着θ角的增大货车对地面的压力增大 | |
| C. | 当货物相对车厢加速下滑时,地面对货车没有摩擦力 | |
| D. | 当货物相对车厢加速下滑时,货车对地面的压力小于货物和货车的总重力 |
4. 质量为M的光滑圆槽放在光滑水平面上,一水平恒力F作用在其上促使质量为m的小球静止在圆槽上,如图所示,则( )
质量为M的光滑圆槽放在光滑水平面上,一水平恒力F作用在其上促使质量为m的小球静止在圆槽上,如图所示,则( )
 质量为M的光滑圆槽放在光滑水平面上,一水平恒力F作用在其上促使质量为m的小球静止在圆槽上,如图所示,则( )
质量为M的光滑圆槽放在光滑水平面上,一水平恒力F作用在其上促使质量为m的小球静止在圆槽上,如图所示,则( )| A. | 小球对圆槽的压力为$\sqrt{(m{g}^{2})+(\frac{mF}{M+m})^{2}}$ | |
| B. | 小球对圆槽的压力为$\frac{mF}{M+m}$ | |
| C. | 水平恒力F变大后,如果小球仍静止在圆槽上,小球对圆槽的压力不变 | |
| D. | 水平恒力F变大后,如果小球仍静止在圆槽上,小球对圆槽的压力减小 |
8.若两个共点力F1和F2的合力为F,则下列说法错误的是( )
| A. | 合力F一定大于任何一个分力 | |
| B. | 合力F的大小可能等于F1 也有可能等于F2 | |
| C. | 合力的大小有可能小于任何一个 | |
| D. | 合力F的大小随着F1和F2间的夹角增大而减小 |
2.用电梯将货物从六楼送到一楼的过程中,货物的v-t图象如图所示.下列说法正确的是( )


| A. | 前2s内货物处于超重状态 | B. | 最后1s内货物只受重力作用 | ||
| C. | 货物在 10s内的平均速度是1.7m/s | D. | 货物在最后1s开始下降 |





 如图所示,ABC为竖直放在电场强度E=104v/m的水平匀强电场中的绝缘光滑轨道,其中轨道的AB部分水平,BC部分是半径R=0.2m的半圆,轨道的水平部分与其半圆相切.A为水平轨道上的一点,把一质量m=0.1kg,带电荷量q=+1×10-4C的小球放在水平轨道的A点由静止开始释放,小球恰好能通过圆轨道的最高点C,g取10m/s2.
如图所示,ABC为竖直放在电场强度E=104v/m的水平匀强电场中的绝缘光滑轨道,其中轨道的AB部分水平,BC部分是半径R=0.2m的半圆,轨道的水平部分与其半圆相切.A为水平轨道上的一点,把一质量m=0.1kg,带电荷量q=+1×10-4C的小球放在水平轨道的A点由静止开始释放,小球恰好能通过圆轨道的最高点C,g取10m/s2.