ЬтФПФкШн
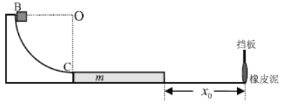
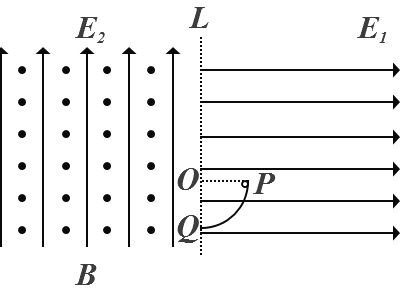
ЁОЬтФПЁПШчЭМЫљЪОЃЌЪњжБЦНУцФкЕФЫФЗжжЎвЛдВЛЁЙьЕРЯТЖЫгыЫЎЦНзРУцЯрЧаЃЌаЁЛЌПщAКЭBЗжБ№ОВжЙдкдВЛЁЙьЕРЕФзюИпЕуКЭзюЕЭЕуЁЃЯжНЋ A ЮоГѕЫйЪЭЗХЃЌA гыBХізВКѓНсКЯЮЊвЛИіећЬхЃЌВЂбизРУцЛЌЖЏЁЃвбжЊдВЛЁЙьЕРЙтЛЌЃЌАыОЖR=0.2mЃЛAКЭBЕФжЪСПОљЮЊm=0.1kgЃЌAКЭBећЬхгызРУцжЎМфЕФЖЏФІВСвђЪ§ =0.2ЁЃШЁжиСІМгЫйЖШ g =10m/s2ЁЃЧѓЃК
ЃЈ1ЃЉгыBХізВЧАЫВМфAЖдЙьЕРЕФбЙСІNЕФДѓаЁЃЛ
ЃЈ2ЃЉХізВЙ§ГЬжаAЖдBЕФГхСПIЕФДѓаЁЃЛ
ЃЈ3ЃЉAКЭBећЬхдкзРУцЩЯЛЌЖЏЕФОрРыlЁЃ

ЁОД№АИЁПЃЈ1ЃЉ3NЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ0.25m
ЃЛЃЈ3ЃЉ0.25m
ЁОНтЮіЁП
ЃЈ1ЃЉЛЌПщAЯТЛЌЕФЙ§ГЬЃЌЛњаЕФмЪиКуЃЌдђга
![]() ЃЌ
ЃЌ
ЛЌПщAдкдВЛЁЙьЕРЩЯзідВжмдЫЖЏЃЌдкзюЕЭЕуЃЌгЩХЃЖйЕкЖўЖЈТЩЕУ
![]()
СНЪНСЊСЂПЩЕУ
FN=3N
гЩХЃЖйЕкШ§ЖЈТЩПЩЕУЃЌAЖдЙьЕРЕФбЙСІ
N=FN=3N
ЃЈ2ЃЉABЯрХіЃЌХізВКѓНсКЯЮЊвЛИіећЬхЃЌгЩЖЏСПЪиКуЕУ
mv=2mvЁф
ЖдЛЌПщBгЩЖЏСПЖЈРэЕУ
![]()
ЃЈ3ЃЉЖдABдкзРУцЩЯЛЌЖЏЃЌЫЎЦНЗНЯђНіЪмФІВССІЃЌдђгЩЖЏФмЖЈРэЕУ
![]()
НтжЎЕУ
l=0.25m