题目内容
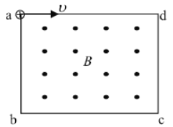
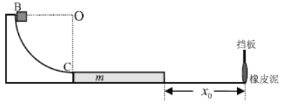
【题目】如图所示，半径为
的四分之一光滑圆弧轨道BC被竖直固定，O为圆心，C为圆轨道的最低点，OC竖直。长为
、质量为
的木板静止在水平面上，其左侧紧邻圆轨道的C点，上表面与C点等高。距木板右侧
处有固定的竖直挡板，挡板上有橡皮泥（木板撞击挡板时会被橡皮泥牢牢粘住）。现有质量为
、可视为质点的物块从B处静止释放。已知物块与木板间的动摩擦因数
，木板与地面间的动摩擦因数
，重力加速度
。求：
(1)物块在C处时对圆轨道的压力；
(2)木板被粘住瞬间，物块距木板左端的距离；
(3)木板与物块、地面间因摩擦而产生的总热量。
【答案】(1)120N，方向竖直向下；(2)2.5m；(3)49.5J
【解析】
(1)物块从B到C有
解得
物块在C处有
解得
由牛顿第三定律可得：物块对轨道的压力大小为120N，方向竖直向下.
(2)物块滑上木板时加速度
由牛顿第二定律可得：
解得木板加速度
设物块经
时间与木板共速
，则
解得
在内，木板位移
物块位移
由于
，说明共速时物块未掉下木板；
又因
，说明木板在末未到达挡板处。
假设之后，M、m一起匀减速运动，其加速度
而物块的摩擦力
故假设成立
故木板被粘住瞬间，物块距木板左端的距离为
(3)一起减速有
解得
木板被粘住后，物块减速到0，有
解得
由于
说明物块停下时还未到达挡板。
物块在时间内与木板间因摩擦生热
木板被粘住后，物块与木板间因摩擦生热
木板与地面间因摩擦生热
故
【题目】关于热力学定律，下列说法中正确的是（ ）
A.可以从单一热源吸收热量，使之完全变为功
B.理想气体的等压膨胀过程一定放热
C.热量不可能从低温物体传递到高温物体
D.压缩气体做功，该气体的内能一定增加
【题目】（1）某同学在做“利用单摆测重力加速度”的实验中，测得的g值偏大，可能的原因是_______________
A．摆球的质量较大 |
B．测周期时，把n次全振动误记为（n+1）次 |
C．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了 |
D．测摆长时，测量摆线长度并加入小球直径 |
（2）某同学在利用单摆测定重力加速度时，由于摆球质量分布不均匀，无法确定其重心位置，他第一次测得单摆振动周期为
，然后将摆长缩短了L，第二次测得振动周期为
（两次实验操作规范），由此可计算出重力加速度g=_________
