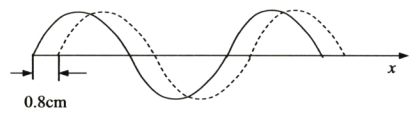
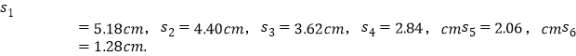��Ŀ����
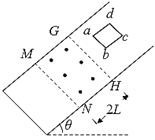
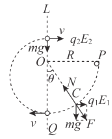
����Ŀ����ͼ��ʾ������L�Ҳ�ռ���ˮƽ���ҵ糡ǿ��E1��2.5N/C����ǿ�糡�����ռ���һ��ֱ���ϵ糡ǿ��E2��1.25N/C����ǿ�糡�ʹ�ֱ��ֽ���������ǿ�ų�B����E1�������ķ�֮һ�Ĺ⻬��ԵԲ������뾶ΪR��0.2m��Բ��������O�㣬���Ͷ˵�Q������ˮƽ���ֽ�һ��Ϊ�ʵ�Ĵ���������Ӵӹ������ߵ�P�ɾ�ֹ�ͷţ������ع����ײ��˶�����֪���ӵ�����Ϊm��1��10��4kg�����Ӵ�����q1��+3��10��4C��ȡg��10m/s2����
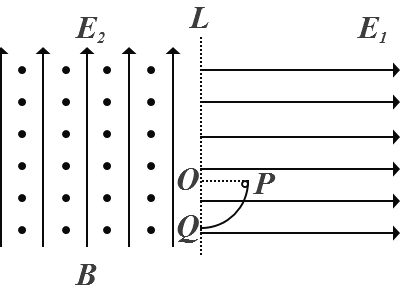
��1�������ع�������˶������жԹ�������ѹ����
��2���������˶���Q��˲���ʹ�������Ϊq2��+8��10��4C��Ҫʹ�����ٴ�ͨ������λ���䵽Բ����ڣ��Ÿ�Ӧǿ��B��СӦ����ʲô������
���𰸡���1��2.25��10��3N����2��B��1T
��������
��1�������ڵ糡E1���ܵ糡��Ϊ�� ![]()
�����������糡��������С![]()
�����ķ�������ֱ�����![]() ��
��![]()
��ã� ![]()
�����ӵ���C��Թ��ѹ��������ʱ�ٶ�Ϊ![]() ����������ӵ�֧����
����������ӵ�֧����![]() ��
��
�ɶ��ܶ����У�![]()
��ţ�ٵڶ������У�![]()
��ã�![]()
��ţ�ٵ������ɿ�֪��P�Թ�����ѹ��Ϊ![]()
��2�����ӵ�������ʱ�ٶ���Ϊ![]()
�ɶ��ܶ����ã�![]()
��ã�![]()
�ڵ糡![]() �У���糡��
�У���糡��![]()
��������L��ิ�ϳ����ܴų�����������Բ���˶����ٴε�![]() ʱ�ٶȴ�С��Ϊ
ʱ�ٶȴ�С��Ϊ![]() ��Ȼ�������糡��������״̬��ͼ
��Ȼ�������糡��������״̬��ͼ
ˮƽ��������Ϊ![]()
���ٶȣ� ![]()
�˶�λ��Ϊ![]() ʱ����Ҫʱ��Ϊ
ʱ����Ҫʱ��Ϊ![]()
����![]()
�������ݽ�ã�![]() ����ȥ����
����ȥ����![]()
��ֱ�����������Լ��ٶ�![]() �������䣬
�������䣬![]() ʱ��������λ�ƣ�
ʱ��������λ�ƣ�![]()
ҪʹB�䵽Բ����ڣ���![]()
�������������䵱��������֪��![]()
������ã�![]()